Bài 1.56 trang 23 SBT hình học 12

Đề bài

Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông ở \(A\) và \(D\), cạnh đáy \(AB = a\), cạnh đáy \(CD = 2a\), \(AD = a\). Hình chiếu vuông góc của \(S\) lên đáy trùng với trung điểm của \(CD\). Biết rằng diện tích mặt bên \(\left( {SBC} \right)\) bằng \(\dfrac{{3{a^2}}}{2}\). Thể tích của hình chóp \(S.ABCD\) bằng:

A. \({a^3}\)                   B. \(\dfrac{{3{a^3}}}{2}\)

C. \(3{a^3}\)                 D. \(3\sqrt 2 {a^3}\)

Lời giải chi tiết

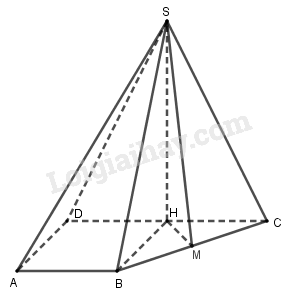
Gọi \(H\) là trung điểm của \(DC\) và \(M\) là trung điểm của \(BC\).

Dễ thấy tam giác \(HBC\) là tam giác vuông cân tại \(H\) có \(HB = HC = a\) thì \(BC = a\sqrt 2 \).

Lại có \({S_{SBC}} = \dfrac{{3{a^2}}}{2}\) \( \Rightarrow SM = \dfrac{{2{S_{SBC}}}}{{BC}} = \dfrac{{2.\dfrac{{3{a^2}}}{2}}}{{a\sqrt 2 }} = \dfrac{{3a\sqrt 2 }}{2}\).

Tam giác \(SHM\) vuông tại \(H\) có \(HM = \dfrac{1}{2}BC = \dfrac{{a\sqrt 2 }}{2}\) và \(SH = \sqrt {S{M^2} - H{M^2}}  = 2a\)

Diện tích hình thang \({S_{ABCD}} = \dfrac{1}{2}\left( {AB + CD} \right).AD\) \( = \dfrac{1}{2}\left( {a + 2a} \right).a = \dfrac{{3{a^2}}}{2}\)

Vậy thể tích \({V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}}.SH\) \( = \dfrac{1}{3}.\dfrac{{3{a^2}}}{2}.2a = {a^3}\).

Chọn A.