Giải Bài 10 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo
Cho hàm số
Đề bài
Cho hàm số \(y = f\left( x \right) = \dfrac{5}{{4x}}\).
a) Tính \(f\left( {\dfrac{1}{5}} \right);f\left( { - 5} \right);f\left( {\dfrac{4}{5}} \right)\).
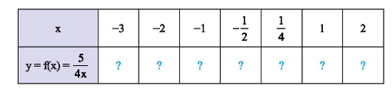
b) Hãy tìm các giá trị tương ứng của hàm số trong bảng sau:
Phương pháp giải - Xem chi tiết
- Giá trị của hàm số tại một điểm \(x = a\) là \(f\left( a \right)\).
Lời giải chi tiết
a) Ta có:
\(f\left( {\dfrac{1}{5}} \right) = \dfrac{5}{{4.\dfrac{1}{5}}} = \dfrac{5}{{\dfrac{4}{5}}} = 5:\dfrac{4}{5} = 5.\dfrac{5}{4} = \dfrac{{25}}{4};\)
\(f\left( { - 5} \right) = \dfrac{5}{{4.\left( { - 5} \right)}} = \dfrac{5}{{ - 20}} = \dfrac{{ - 1}}{4};\)
\(f\left( {\dfrac{4}{5}} \right) = \dfrac{5}{{4.\dfrac{4}{5}}} = \dfrac{5}{{\dfrac{{16}}{5}}} = 5:\dfrac{{16}}{5} = 5.\dfrac{5}{{16}} = \dfrac{{25}}{{16}}\)
b) Ta có:
\(f\left( { - 3} \right) = \dfrac{5}{{4.\left( { - 3} \right)}} = \dfrac{5}{{ - 12}} = \dfrac{{ - 5}}{{12}};\)
\(f\left( { - 2} \right) = \dfrac{5}{{4.\left( { - 2} \right)}} = \dfrac{5}{{ - 8}} = \dfrac{{ - 5}}{8};\)
\(f\left( { - 1} \right) = \dfrac{5}{{4.\left( { - 1} \right)}} = \dfrac{5}{{ - 4}} = \dfrac{{ - 5}}{4};\)
\(f\left( { - \dfrac{1}{2}} \right) = \dfrac{5}{{4.\left( { - \dfrac{1}{2}} \right)}} = \dfrac{5}{{\dfrac{{ - 4}}{2}}} = \dfrac{5}{{ - 2}} = \dfrac{{ - 5}}{2}\);
\(f\left( {\dfrac{1}{4}} \right) = \dfrac{5}{{4.\dfrac{1}{4}}} = \dfrac{5}{{\dfrac{4}{4}}} = \dfrac{5}{1} = 5\);
\(f\left( 1 \right) = \dfrac{5}{{4.1}} = \dfrac{5}{4}\);
\(f\left( 2 \right) = \dfrac{5}{{4.2}} = \dfrac{5}{8}\)
Ta có bảng sau:
|
\(x\) |
–3 |
–2 |
–1 |
\( - \dfrac{1}{2}\) |
\(\dfrac{1}{4}\) |
1 |
2 |
|
\(y = f\left( x \right) = \dfrac{5}{{4x}}\) |
\(\dfrac{{ - 5}}{{12}}\) |
\(\dfrac{{ - 5}}{8}\) |
\(\dfrac{{ - 5}}{4}\) |
\(\dfrac{{ - 5}}{2}\) |
5 |
\(\dfrac{5}{4}\) |
\(\dfrac{5}{8}\) |
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải Bài 10 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo timdapan.com"