Đề kiểm tra 15 phút - Đề số 9 - Bài 7 - Chương 3 – Hình học 7

Đề bài

Cho điểm M nằm trong góc \(\widehat {xOy}\), lấy các điểm A và B sao cho Ox là đường trung trực của MA và Oy là đường trung trực của MB. Chứng minh: O là trung điểm của đoạn AB. 

Lời giải chi tiết

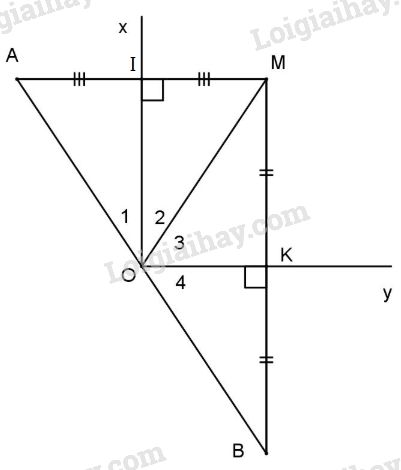
Ox là đường trung trực của AM (gt) ta có OA = OM.

Tương tự Oy là trung trực của BM: \(OB = OM \Rightarrow OA = OB\) (1).

Gọi I là giao điểm của Ox và AM ta có:

\(\Delta AI{\rm{O}} = \Delta MI{\rm{O}}\) (c.c.c) \( \Rightarrow {\widehat O_1} = {\widehat O_2}.\)

Chứng minh tương tự ta có \({\widehat O_3} = {\widehat O_4},\) mà \({\widehat O_2} + {\widehat O_3} = {90^0} \)

\(\Rightarrow {\widehat O_1} + {\widehat O_2} + {\widehat O_3} + {\widehat O_4} = {180^0}.\)

Chứng tỏ ba điểm A, O, B thẳng hàng (2).

Từ (1) và (2) suy ra O là trung điểm của đoạn AB.