Bài 47 trang 76 SGK Toán 7 tập 2

Đề bài

Cho hai điểm \(M, N\) nằm trên đường trung trực của đoạn thẳng \(AB\). Chứng minh \(∆AMN  = ∆BMN.\)

Lời giải chi tiết

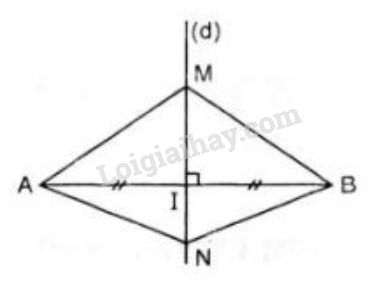
Vì \(M\) thuộc đường trung trực của \(AB\) nên \(MA = MB\) (Theo định lí \(1\))

\(N\) thuộc đường trung trực của \(AB\) nên \(NA = NB\) (Theo định lí \(1\))

Xét \(∆AMN\) và \(∆BMN\) ta có:

+) \(MA = MB\) (chứng minh trên)

+) \(NA = NB\) (chứng minh trên)

+) \(MN\) chung

Vậy \(∆AMN  = ∆BMN\) (c.c.c) (điều phải chứng minh).