Đề kiểm tra 15 phút - Đề số 10 - Bài 7 - Chương 3 – Hình học 7

Đề bài

Cho tam giác ABC cân tại A, lấy D trên tia đối của tia BC sao cho \(BD = BA\), lấy E trên tia đối của tia CB sao cho \(CE = CA\). Kẻ trung tuyến BM của tam giác ABD và CN của tam giác ACE, BM cắt CN tại O. Chứng minh rằng \(AO \bot DE\).

Lời giải chi tiết

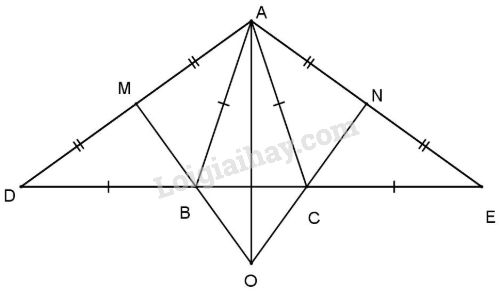
Ta có \(BD = BA\) (gt) nên \(\Delta AB{\rm{D}}\) cân tại B. Do đó trung tuyến BM đồng thời là đường trung trực của AD.

Chứng minh tương tự ta có CN cũng là trung trực của AE, mà BM cắt CN tại O nên O là giao điểm hai đường trung trực của \(\Delta A{\rm{D}}E\).

Vì vậy OA phải là đường trung trực thứ ba của \(\Delta A{\rm{D}}E\) hay \(OA \bot DE.\)