Bài 8 trang 94 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho đường tròn (O; r) có đường kính AB. Lấy trên cung AB hai điểm C, D sao cho các tia AC,
Đề bài
Cho đường tròn (O; r) có đường kính AB. Lấy trên cung AB hai điểm C, D sao cho các tia AC, BD cắt nhau tại điểm M ở ngoài đường tròn. Vẽ đường tròn (O’) qua M, C, D. Chứng minh MO’ vuông góc với AB.
Phương pháp giải - Xem chi tiết
+) Vẽ đường kính MI của đường tròn \(\left( {O'} \right)\).
+) Chứng minh IC và BC cùng vuông góc với MC, suy ra B; I; C thẳng hàng, BC là đường cao của tam giác ABC.
+) Chứng minh tương tự A; I; D thẳng hàng, AD là đường cao của tam giác ABC.
+) Chứng minh I là trực tâm của tam giác ABC, từ đó suy ra điều phải chứng minh.
Lời giải chi tiết
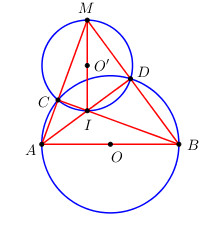
Vẽ đường kính MI của đường tròn \(\left( {O'} \right)\).
Xét đường tròn \(\left( {O'} \right)\) ta có \(\widehat {MCI}\) là góc nội tiếp chắn nửa đường tròn \( \Rightarrow \widehat {MCI} = {90^0} \Rightarrow IC \bot MC\)
Xét đường tròn \(\left( O \right)\) ta có \(\widehat {ACB}\) là góc nội tiếp chắn nửa đườn tròn \( \Rightarrow \widehat {ACB} = {90^0} \Rightarrow BC \bot AC\)hay \(BC \bot MC\).
Theo tiên đề Ơ-lít ta có B; I; C thẳng hàng, BC là đường cao của tam giác ABC.
Chứng minh hoàn toàn tương tự ta có A; I; D thẳng hàng, AD là đường cao của tam giác ABC.
\(BC \cap AD = I \Rightarrow I\) là trực tâm của tam giác ABC \( \Rightarrow MI \bot AB\).
Mà \(O' \in MI \Rightarrow MO' \bot AB\).
Vậy \(MO' \bot AB\) (đpcm).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 8 trang 94 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







