Bài 2 trang 94 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho đường tròn (O) đường kính AB vuông góc với dây CD tại E.
Đề bài
Cho đường tròn (O) đường kính AB vuông góc với dây CD tại E.
Chứng minh: \(C{D^2} = 4AE.BE\)
Phương pháp giải - Xem chi tiết
+) Chứng minh tam giác ABC vuông tại C, sử dụng hệ thức lượng trong tam giác vuông tính CE theo AE và BE.
+) Sử dụng quan hệ vuông góc giữa đường kính và dây cung chứng minh E là trung điểm của CD \( \Rightarrow CD = 2CE\).
Lời giải chi tiết
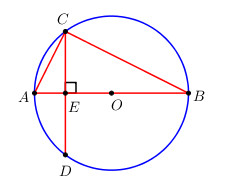
Ta có \(\widehat {ACB}\) là góc nội tiếp chắn nửa đường tròn \( \Rightarrow \widehat {ACB} = {180^0} \Rightarrow \Delta ABC\) vuông tại C.
Áp dụng hệ thức lượng trong tam giác vuông ABC có: \(C{E^2} = AE.BE\).
Ta có: \(AB \bot CD\) tại E \( \Rightarrow E\) là trung điểm của CD (Quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow CD = 2CE \) \(\Rightarrow C{D^2} = 4C{E^2} = 4AE.BE\) (đpcm).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2 trang 94 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







