Bài 7 trang 115 SGK Toán 11 tập 2 - Cánh Diều
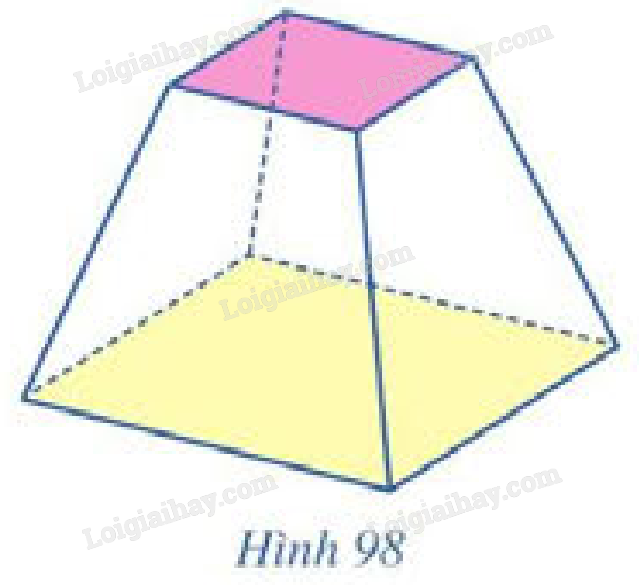
Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều (Hình 98).
Đề bài
Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều (Hình 98). Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 3 m. Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m . Tính số tiền để mua bê tông tươi làm chân tháp theo đơn vị đồng.
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).
Lời giải chi tiết

Mô hình hoá chân tháp bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy. Vậy \(AB = 5,A'B' = 2,CC' = 3\).
\(ABCD\) là hình vuông
\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = 5\sqrt 2 \Rightarrow CO = \frac{1}{2}AC = \frac{{5\sqrt 2 }}{2}\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow A'C' = \sqrt {A'B{'^2} + B'C{'^2}} = 2\sqrt 2 \Rightarrow C'O' = \frac{1}{2}A'C' = \sqrt 2 \)
Kẻ \(C'H \bot OC\left( {H \in OC} \right)\)
\(OHC'O'\) là hình chữ nhật \( \Rightarrow OH = O'C' = \sqrt 2 ,OO' = C'H \Rightarrow CH = OC - OH = \frac{{3\sqrt 2 }}{2}\)
\(\Delta CC'H\) vuông tại \(H \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}} = \frac{{3\sqrt 2 }}{2} \Rightarrow OO' = C'H = \frac{{3\sqrt 2 }}{2}\)
Diện tích đáy lớn là: \(S = A{B^2} = {5^2} = 25\left( {{m^2}} \right)\)
Diện tích đáy bé là: \(S' = A'B{'^2} = {2^2} = 4\left( {{m^2}} \right)\)
Thể tích hình chóp cụt là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.\frac{{3\sqrt 2 }}{2}\left( {25 + \sqrt {25.4} + 4} \right) = \frac{{39\sqrt 2 }}{2}\left( {{m^3}} \right)\)
Số tiền để mua bê tông tươi làm chân tháp là: \(\frac{{39\sqrt 2 }}{2}.1470000 \approx 40538432\) (đồng).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7 trang 115 SGK Toán 11 tập 2 - Cánh Diều timdapan.com"







