Bài 6 trang 99 SGK Toán 11 tập 2 - Cánh Diều
Cho lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh cùng bằng \(a\), hai mặt phẳng \(\left( {A'AB} \right)\) và \(\left( {A'AC} \right)\)
Đề bài
Cho lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh cùng bằng \(a\), hai mặt phẳng \(\left( {A'AB} \right)\) và \(\left( {A'AC} \right)\) cùng vuông góc với \(\left( {ABC} \right)\).
a) Chứng minh rằng \(AA' \bot \left( {ABC} \right)\).
b) Tính số đo góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {ABC} \right)\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng định lí: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
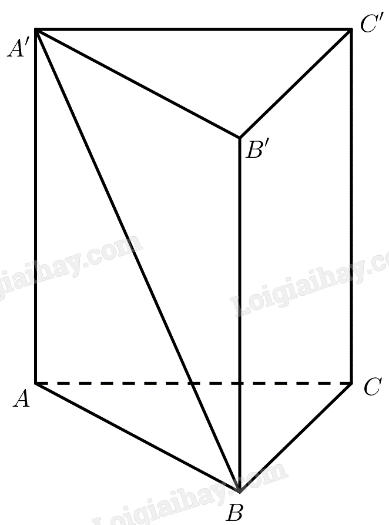
a) Ta có:
\(\left. \begin{array}{l}\left( {A'AB} \right) \bot \left( {ABC} \right)\\\left( {A'AC} \right) \bot \left( {ABC} \right)\\\left( {A'AB} \right) \cap \left( {A'AC} \right) = AA'\end{array} \right\} \Rightarrow AA' \bot \left( {ABC} \right)\)
b) \(AA' \bot \left( {ABC} \right) \Rightarrow \left( {A'B,\left( {ABC} \right)} \right) = \left( {A'B,AB} \right) = \widehat {ABA'}\)
\(\Delta AA'B\) vuông tại \(A\) có \(\tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {ABA'} = {45^ \circ }\)
Vậy \(\left( {A'B,\left( {ABC} \right)} \right) = {45^ \circ }\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 6 trang 99 SGK Toán 11 tập 2 - Cánh Diều timdapan.com"







