Bài 42 trang 97 SGK Đại số10 nâng cao

Cho hai đường thẳng (\(d_1\)): x + my = 3 và (\(d_2\)): mx + 4y = 6.

LG a

Với giá trị nào của m thì hai đường thẳng đó cắt nhau?

Lời giải chi tiết:

Xét hệ phương trình tọa độ giao điểm: 

\(\left\{ \matrix{
x + my = 3 \hfill \cr 
mx + 4y = 6 \hfill \cr} \right.\)

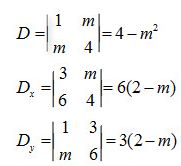
(d₁) và (d₂) cắt nhau ⇔ hệ có nghiệm duy nhất

⇔ D ≠ 0 \( \Leftrightarrow 4 - {m^2} \ne 0\)⇔ m ≠ ±2

LG b

 Với giá trị nào của m thì hai đường thẳng ấy song song với nhau?

Lời giải chi tiết:

(d₁)//(d₂) ⇔ hệ vô nghiệm

⇔ D = 0 và D_x ≠ 0 hoặc (D_y ≠ 0)

\( \Leftrightarrow \left\{ \begin{array}{l}
4 - {m^2} = 0\\
\left[ \begin{array}{l}
6\left( {2 - m} \right) \ne 0\\
3\left( {2 - m} \right) \ne 0
\end{array} \right.
\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}
m = \pm 2\\
m \ne 2
\end{array} \right. \Leftrightarrow m = - 2\)

LG c

Với giá trị nào của m thì hai đường thẳng ấy trùng nhau?

Lời giải chi tiết:

(d₁) trùng với (d₂) ⇔ hệ vô số nghiệm

⇔ D = D_x = D_y = 0

\( \Leftrightarrow \left\{ \begin{array}{l}
4 - {m^2} = 0\\
6\left( {2 - m} \right)= 0\\
3\left( {2 - m} \right)= 0
\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}
m = \pm 2\\
m = 2
\end{array} \right. \Leftrightarrow m =  2\)