Bài 4.11 trang 82 SGK Toán 11 tập 1 - Kết nối tri thức
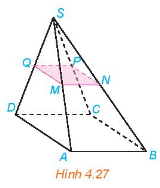
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình bình hành
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình bình hành,
Phương pháp giải - Xem chi tiết
Dấu hiệu nhận biết tứ giác là hình bình hành khi có 2 cặp cạnh tương ứng song song với nhau.
Lời giải chi tiết
Xét tam giác SAB ta có: MN là đường trung bình suy ra MN // AB.
Tương tự ta có: NP // BC, PQ // CD, MQ // AD.
Mà ABCD là hình bình hành nên AB // CD, AD// CD, suy ra MN // PQ, MQ // NP.
Như vậy, MNPQ là hình bình hành.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4.11 trang 82 SGK Toán 11 tập 1 - Kết nối tri thức timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4.11 trang 82 SGK Toán 11 tập 1 - Kết nối tri thức timdapan.com"







