Bài 30 trang 66 SGK Hình học 10 nâng cao

Đề bài

Cho tứ giác \(ABCD\). Gọi \(M, N\) lần lượt là trung điểm của \(AC\) và \(BD\). Chứng minh rằng \(A{B^2} + B{C^2} + C{D^2} + D{A^2} = A{C^2} + B{D^2} + 4M{N^2}\).

Lời giải chi tiết

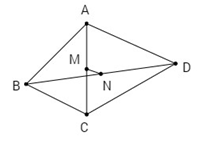
Áp dụng công thức tính trung tuyến, \(MN\) là trung tuyến của tam giác \(BMD\), ta có

\(M{N^2} = {{B{M^2} + D{M^2}} \over 2} - {{B{D^2}} \over 4}\,\,\,\,\, \Leftrightarrow \,\,4M{N^2} = 2(B{M^2} + D{M^2}) - B{D^2}\,\,\,(1)\)

Tương tự, \(BM, DM\) lần lượt là trung tuyến của tam giác \(ABC, ADC\) nên

\(\eqalign{
& 4B{M^2} = 2(A{B^2} + B{C^2}) - A{C^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2) \cr 
& 4D{M^2} = 2(D{A^2} + C{D^2}) - A{C^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3) \cr} \)

Từ (2), (3) suy ra

\(2(B{M^2} + D{M^2}) = A{B^2}\, + B{C^2} + C{D^2} + D{A^2} - A{C^2}\,\,(4)\)

Thay (4) vào (1), ta có

\(\eqalign{
& \,\,\,\,\,\,\,\,4M{N^2} = A{B^2} + B{C^2} + C{D^2} + D{A^2} - A{C^2} - B{D^2} \cr 
& \Rightarrow \,\,\,A{B^2} + B{C^2} + C{D^2} + D{A^2} = A{C^2} + B{D^2} + 4M{N^2} \cr} \)