Đề kiểm tra học kì 1 môn Toán lớp 10
Đề kiểm tra học kì 1 môn Toán lớp 10 năm học 2014 - 2015 trường THPT Châu Thành 1, Đồng Tháp là đề thi học kì I lớp 10 môn Toán có đáp án đi kèm. Hi vọng tài liệu này sẽ giúp các bạn củng cố kiến thức môn Toán, luyện đề nhằm chuẩn bị sẵn sàng cho kì thi học kì 1 sắp tới.
Đề cương ôn tập học kì 1 môn Toán lớp 10 trường THPT Đa Phúc, Hà Nội năm học 2016 - 2017
Bảng công thức lượng giác dùng cho lớp 10 - 11 - 12
Đề thi học kì 1 môn Tiếng Anh lớp 10 trường THPT Châu Thành 1, Đồng Tháp năm 2014 - 2015
Đề kiểm tra học kì 1 môn Ngữ văn lớp 10 năm học 2014 - 2015 trường THPT Châu Thành 1, Đồng Tháp
| SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH ĐỒNG THÁP
ĐỀ CHÍNH THỨC (Đề gồm có 01 trang) | KIỂM TRA HỌC KÌ I Năm học: 2014-2015 Môn thi: TOÁN - Lớp 10 Ngày thi: 25/12/2014 Thời gian: 90 phút (không kể thời gian phát đề) |
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (8,0 điểm)
Câu I. (1,0 điểm)
Cho hai tập hợp A = {0; 1; 3; 4}, B = {1; 3; 5}. Tìm A υ B và A ∩ B.
Câu II. (2,0 điểm)
1. Tìm parabol (P): y = ax2 + bx + 2 (a ≠0), biết parabol đó có trục đối xứng là x = 3/2 và đi qua điểm A(-1; 6).
2. Lập bảng biến thiên và vẽ đồ thị hàm số: y = -x2 + 2x - 1.
Câu III. (3,0 điểm)
1. Giải phương trình: ![]()
2. Giải phương trình: 4x4 - 65x2 + 16 = 0.
3. Không sử dụng máy tính, hãy giải hệ phương trình: ![]()
Câu IV. (2,0 điểm)
Trong mặt phẳng tọa độ Oxy, cho tam giác MNP có M(3; 0), N(-1; -1), P(1; 2).
1. Tìm tọa độ trọng tâm G của ΔMNP và tọa độ ![]() .
.
2. Tìm tọa độ đỉnh Q sao cho tứ giác MNPQ là hình bình hành.
II. PHẦN RIÊNG - Tự chọn (2,0 điểm)
Học sinh chỉ được chọn một trong hai phần (phần 1 hoặc phần 2)
Phần 1: Theo chương trình Chuẩn.
Câu V.a. (1,0 điểm)
Cho a ≥ 1; b ≥ 1. Chứng minh bất đẳng thức: ![]()
Câu VI.a. (1,0 điểm)
Cho tam giác ABC có A(1; 2), B(–2; 6), C(9; 8). Tìm tọa độ trực tâm H của ΔABC.
Phần 2: Theo chương trình nâng cao.
Câu V.b.
Giải phương trình:
![]()
Câu VI.b. (1,0 điểm)
Cho tam giác ABC có A(–4; 5), B(–2; 0), C(1; 3). Biết AH là đường cao của ΔABC(H ∈ BC). Tìm tọa độ H.
Đáp án đề kiểm tra học kì 1 môn Toán lớp 10
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (8,0 điểm)
Câu I. (1,0 điểm)
A υ B = {0; 1; 3; 4; 5}
A ∩ B = {1; 3}
Câu II. (2,0 điểm)
1. x = 3/2 là trục đối xứng → -b/2a = 3/2 ↔ 3a + b = 0 (1)
P đi qua A(-1; 6) → a - b = 4 (2)
Hệ: ![]()
Vậy (P): y = x2 - 3x + 2
2. D = R; Tọa độ đỉnh I(1; 0).
Trục đối xứng là đường thẳng x = 1. Do a = -1 < 0 nên (P) có bề lõm hướng xuống.
Bảng biến thiên
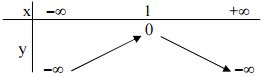
Đồ thị

Câu III. (3,0 điểm)
1. Giải phương trình ![]() (*)
(*)

Vậy tập nghiệm là S = {3}
2. Đặt t = x2 (t ≥ 0). Phương trình trở thành: 4t2 - 65t + 16 = 0
↔ t = 16 hoặc t = 1/4 (thỏa đk)
+ t = 16 ↔ x2 = 16 ↔ x = ± 4
+ t = 1/4 ↔ x2 = 1/4 ↔ x = ±1/2
Vậy phương trình có 4 nghiệm: x = ±1/2; x = ±4
3. 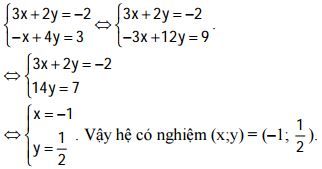
Câu IV. (2,0 điểm)
1. G(x; y) là trọng tâm ΔMNP nên 
![]()
2. Gọi Q(x; y)
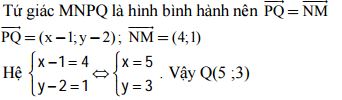
II. PHẦN RIÊNG - Tự chọn (2,0 điểm)
Phần 1: Theo chương trình Chuẩn.
Câu V.a. (1,0 điểm)

Câu VI.a. (1,0 điểm)
Gọi H(x; y)
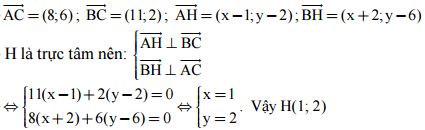
Phần 2: Theo chương trình nâng cao.
Câu V.b.
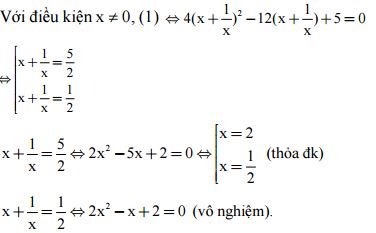
Vậy phương trình đã cho có hai nghiệm x = 2, x = 1/2
Câu VI.b. (1,0 điểm)
Gọi H(x; y)