Giải mục 4 trang 91, 92, 93 SGK Toán 11 tập 1 - Kết nối tri

Hoạt động 6

Các hình ảnh dưới đây có đặc điểm chung nào với hình lăng trụ đứng tam giác mà em đã học ở lớp 7? 

Phương pháp giải:

Dựa vào dấu hiệu hình lăng trụ đứng tam giác ta có thể tìm đặc điểm chung.

Lời giải chi tiết:

- Các cạnh bên của hình lăng trụ đứng vuông góc với đáy.

- Những mặt phẳng chứa đáy song song với nhau.

Luyện tập 5

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’. Chứng minh rằng AMC.A’M’C’ là hình lăng trụ.

Phương pháp giải:

Cách chứng minh lăng trụ

- Hai mặt đáy của lăng trụ song song nhau.

- Các mặt bên của hình lăng trụ là hình bình hành.

- Các cạnh bên song song, bằng nhau và tạo với đáy các góc bằng nhau.

Lời giải chi tiết:

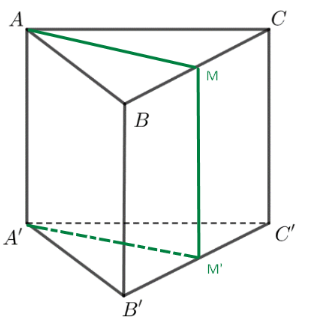
Ta có M, M' lần lượt là trung điểm của BC, B'C', BCC'B' là hình bình hành suy ra MM' // CC'.

Vì các cạnh bên của hình lăng trụ ABC.A'B'C' đôi một song song nên AA'//CC'.

Mặt phẳng ((AMC) //(A'M'C') nên AMC. AM'C' là hình lăng trụ.

Hoạt động 7

Hình ảnh nào trong HĐ6 gợi nên hình ảnh về hình lăng trụ có đáy là hình bình hành?

Phương pháp giải:

Hình bình hành là hình có các cặp cạnh đối song song và bằng nhau.

Lời giải chi tiết:

Hình số 2.

Luyện tập 6

Cho hình hộp ABCD.A’B’C’D. Chứng minh rằng hai mặt phẳng (ADD’A’) và (BCC’B’) song song với nhau.

Phương pháp giải:

Để chứng minh hai mặt phẳng song song, ta dựa vào tính chất của hình hộp và hình bình hành:

Hai mặt đối diện của hình hộp là hai mặt không có điểm chung nên song song với nhau.

Lời giải chi tiết:

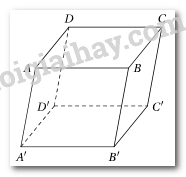
Ta có: ABCD là hình bình hành suy ra AD // BC suy ra AD // (BCC'B').

ABCD.A'B'C'D' là hình hộp suy ra DD'//CC' suy ra DD' // (BCC'B').

(ADD'A') chứa cặp cạnh cắt nhau song song với (BCC'B') nên (ADD'A') //(BCC'B').

Vận dụng 2

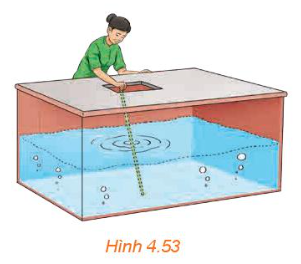
Để xác định mực nước trong một chiếc bể có dạng hình hộp, bác Hà đặt một thanh gỗ đủ dài vào trong bể sao cho một đầu của thanh gỗ dựa vào mép của nắp bể, đầu còn lại nằm trên đáy bể (H.4.53). Sau đó bác Hà rút thanh gỗ ra ngoài và tính tỉ lệ giữa độ dài của phần thanh gỗ bị ngâm trong nước và độ dài của cả thanh gỗ. Tỉ lệ này chính bằng tỉ lệ giữa mực nước và chiều cao của bể. Hãy giải thích vì sao.

Phương pháp giải:

Áp dụng định lí Thales trong không gian để giải thích sự bằng nhau giữa các tỉ lệ này.

Lời giải chi tiết:

Mặt nước, nắp bể và đáy bể đôi một song với nhau song song với nhau, thanh gỗ đóng vai trò là cắt tuyến cắt các mặt phẳng đáy bể tại đầu thứ nhất của thanh gỗ, cắt mặt nước giao điểm giữa phần ngâm nước và phần chưa ngâm nước của thanh gỗ, cắt nắp bể tại đầu còn lại của thanh gỗ.

Áp dụng định lí Thales, ta có tỉ lệ giữa độ dài của phân thanh gỗ bị ngâm trong nước và độ dài của cả thanh gỗ bằng tỉ lệ giữa mực nước và chiều cao của bể.