Bài 4.27 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức
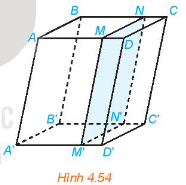
Cho hình hộp ABCD.A’B’C’D’. Một mặt phẳng song song với mặt bên (ABB’A’) của hình hộp và cắt các cạnh AD, BC, A’D, B’C’ lần lượt tại M, N, M’, N’ (H.4.54). Chứng minh rằng ABNM.A’B’N’M” là hình hộp
Đề bài
Cho hình hộp ABCD.A’B’C’D’. Một mặt phẳng song song với mặt bên (ABB’A’) của hình hộp và cắt các cạnh AD, BC, A’D, B’C’ lần lượt tại M, N, M’, N’ (H.4.54).
Chứng minh rằng ABNM.A’B’N’M” là hình hộp.
Phương pháp giải - Xem chi tiết
Hình lăng trụ tứ giác có hai đáy là hình bình hành được gọi là hình hộp.
Lời giải chi tiết
\( - \;\)Ta có \(\left( {ABB'C'} \right)\;//\;\left( {MNN'M'} \right),\;\left( {ADD'A'} \right) \cap \left( {ABB'A'} \right) = AA',\left( {ADD'A'} \right) \cap \left( {MNN'M'} \right) = MM'\)
suy ra AA'//MM'
Tương tự, BB' // NN'
ABNM.A'B'N'M' có các cạnh bên đôi một song song, (ABNM) //(A'B'N'M')
Suy ra ABNM.A'B'C'M' là hình lăng trụ.
\( - \;\)Ta có: \(\left( {ABB'C'} \right)\;//\;\left( {MNN'M'} \right),\;\left( {ABNM} \right) \cap \left( {ABB'A'} \right) = AB,\left( {ABNM} \right) \cap \left( {MNN'M'} \right) = MN\)
Suy ra AB//MN.
Ta có có AB // MN, BN// AM nên tứ giác ABNM là hình bình hành.
Do đó ABNM.A'B'C'M' là hình hộp.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4.27 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức timdapan.com"







