Giải mục 3 trang 16, 17 SGK Toán 11 tập 2 - Chân trời sáng tạo
Cho các số thực dương (a,M,N) với (a ne 1). Bạn Quân đã vẽ sơ đồ và tìm ra công thức biến đổi biểu thức ({log _a}left( {MN} right)) như sau:
Hoạt động 2
Cho các số thực dương \(a,M,N\) với \(a \ne 1\). Bạn Quân đã vẽ sơ đồ và tìm ra công thức biến đổi biểu thức \({\log _a}\left( {MN} \right)\) như sau:
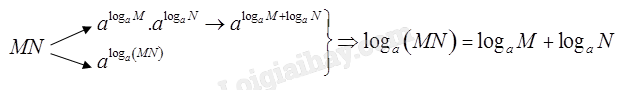
a) Giải thích cách làm của bạn Quân.
b) Vẽ sơ đồ tương tự để tìm công thức biến đổi cho \({\log _a}\frac{M}{N}\) và \({\log _a}{M^\alpha }\left( {\alpha \in \mathbb{R}} \right)\).
Phương pháp giải:
Sử dụng định nghĩa của lôgarit.
Lời giải chi tiết:
a) Ta có: \(M = {a^{{{\log }_a}M}},N = {a^{{{\log }_a}N}} \Rightarrow MN = {a^{{{\log }_a}M}}.{a^{{{\log }_a}N}} = {a^{{{\log }_a}M + {{\log }_a}N}}\)
Mặt khác: \(MN = {a^{{{\log }_a}\left( {MN} \right)}}\)
Vậy \({a^{{{\log }_a}M + {{\log }_a}N}} = {a^{{{\log }_a}\left( {MN} \right)}} \Leftrightarrow {\log _a}M + {\log _a}N = {\log _a}\left( {MN} \right)\)
b)
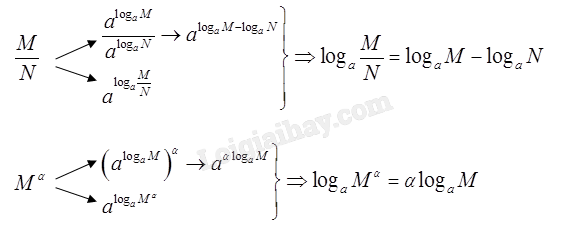
Thực hành 3
Tính:
a) \({\log _5}4 + {\log _5}\frac{1}{4}\);
b) \({\log _2}28 - {\log _2}7\); c) \(\log \sqrt {1000} \).
Phương pháp giải:
Sử dụng các tính chất của phép tính lôgarit.
Lời giải chi tiết:
a) \({\log _5}4 + {\log _5}\frac{1}{4} = {\log _5}\left( {4.\frac{1}{4}} \right) = {\log _5}1 = 0\).
b) \({\log _2}28 - {\log _2}7 = {\log _2}\frac{{28}}{7} = {\log _2}4 = {\log _2}{2^2} = 2\).
c) \(\log \sqrt {1000} = \log {1000^{\frac{1}{2}}} = \log {\left( {{{10}^3}} \right)^{\frac{1}{2}}} = \log {10^{\frac{3}{2}}} = \frac{3}{2}\).
Vận dụng
Độ lớn \(M\) của một trận động đất theo thang Richter được tính theo công thức \(M = \log \frac{A}{{{A_0}}}\), trong đó \(A\) là biên độ lớn nhất ghi được bởi máy đo địa chấn, \({A_0}\) là biên độ tiêu chuẩn được sử dụng để hiệu chỉnh độ lệch gây ra bởi khoảng cách của máy đo địa chấn so với tâm chấn (ở Hoạt động mở đầu và Hoạt động 1, \({A_0} = 1\mu m\)).
a) Tính độ lớn của trận động đất có biên độ \(A\) bằng
i) \({10^{5,1}}{A_0}\); ii) \(65000{A_0}\).
b) Một trận động đất tại địa điểm \(N\) có biên độ lớn nhất gấp ba lần biên độ lớn nhất của trận động đất tại địa điểm \(P\). So sánh độ lớn của hai trận động đất.
Phương pháp giải:
Thay vào công thức tính độ lớn \(M\) và sử dụng tính chất của lôgarit.
Lời giải chi tiết:
a) Với \(A = {10^{5,1}}{A_0}\), ta có: \(M = \log \frac{A}{{{A_0}}} = \log \frac{{{{10}^{5,1}}{A_0}}}{{{A_0}}} = \log {10^{5,1}} = 5,1\) (Richter).
Với \(A = 65000{A_0}\), ta có: \(M = \log \frac{A}{{{A_0}}} = \log \frac{{65000{A_0}}}{{{A_0}}} = \log 65000 \approx 4,81\) (Richter).
b) Với \({A_N} = 3{A_P}\), ta có: \({M_N} = \log \frac{{{A_N}}}{{{A_0}}},{M_P} = \log \frac{{{A_P}}}{{{A_0}}}\).
\({M_N} - {M_P} = \log \frac{{{A_N}}}{{{A_0}}} - \log \frac{{{A_P}}}{{{A_0}}} = \log \left( {\frac{{{A_N}}}{{{A_0}}}:\frac{{{A_P}}}{{{A_0}}}} \right) = \log \frac{{{A_N}}}{{{A_P}}} = \log \frac{{3{A_N}}}{{{A_P}}} = \log 3 \approx 0,48\)
Vậy trận động đất tại địa điểm \(N\) lớn hơn trận động đất tại địa điểm \(P\) 0,48 Richter.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 3 trang 16, 17 SGK Toán 11 tập 2 - Chân trời sáng tạo timdapan.com"







