Giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều
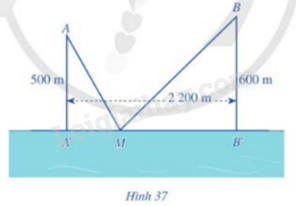
Có hai xã A,B cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA’ =500m, BB’=600m và người ta đo được A’B’= 2.200m(hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A’B’ sao cho tổng khoảng cách từ hai xa đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
Đề bài
Có hai xã A,B cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA’ =500m, BB’=600m và người ta đo được A’B’= 2.200m(hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A’B’ sao cho tổng khoảng cách từ hai xa đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
Phương pháp giải - Xem chi tiết
+, Phân tích đề bài
+, Tìm mối liên hệ tròng bài
Lời giải chi tiết
Để tiết kiệm chi phí xây dựng ta lấy điểm I đối xứng với điểm A qua A’
Kẻ đường thẳng IB ta được: \(\Delta AA'M\)~\(\Delta BB'M\)
\(\frac{{AA'}}{{BB'}} = \frac{{AM}}{{BM}} = \frac{{A'M}}{{B'M}} = \frac{5}{6}\;\;\;\;\;\;\)
=> \(A'M = \frac{5}{6}B'M\) (1)
Mặt khác A’M +B’M =2200 (2)
Từ (1), (2) ta có \(\left\{ {\begin{array}{*{20}{c}}{A'M = 1000}\\{B'M = 1200}\end{array}} \right.\)
=>\(\left\{ {\begin{array}{*{20}{c}}{AM = \sqrt {A{A^{'2}} + A'{M^2}} = 500\sqrt 5 m}\\{BM = \sqrt {B{B^{'2}} + B'{M^2}} = 600\sqrt 5 m}\end{array}} \right.\)
=> khoảng cách ngắn nhất là đoạn AM +MB =1100\(\sqrt 5 \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều timdapan.com"







