Bài 81* trang 51 SBT toán 7 tập 2
Giải bài 81* trang 51 sách bài tập toán 7. Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF (h.17) a) Chứng minh rằng A là trung điểm EF...
Đề bài
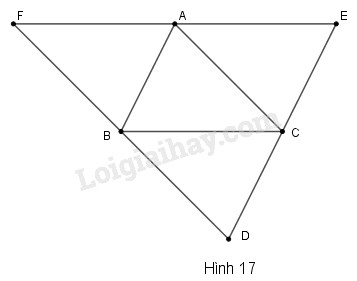
Cho tam giác \(ABC.\) Qua mỗi đỉnh \(A, B, C\) kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác \(DEF\) (h.17)
a) Chứng minh rằng \(A\) là trung điểm \(EF.\)
b) Các đường cao của tam giác \(ABC\) là các đường trung trực của tam giác nào?
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Tính chất hai tam giác bằng nhau
+) Quan hệ từ vuông góc đến song song
+) Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm đoạn thẳng ấy.
Lời giải chi tiết

a) Xét \(∆ABC\) và \(∆CEA\) có:
+) \(\widehat {ACB} = \widehat {CA{\rm{E}}}\) (so le trong, \(AE // BC)\)
+) \(AC\) cạnh chung
+) \(\widehat {CAB} = \widehat {AC{\rm{E}}}\) (so le trong,\( CE // AB)\)
Do đó: \(∆ABC = ∆CEA\) (g.c.g)
\( \Rightarrow AE = BC\) (1)
Xét \(∆BAC\) và \(∆ABF\) có:
+) \(\widehat {ABC} = \widehat {{\rm{BAF}}}\) (so le trong, \(BF // AC)\)
+) \(AB\) cạnh chung
+) \(\widehat {BAC} = \widehat {ABF}\) (so le trong, \(BF // AC)\)
Do đó: \(∆BAC = ∆ABF\) (g.c.g)
\( \Rightarrow AF = BC \) (2)
Từ (1) và (2) suy ra: \(AE = AF.\) Vậy \(A\) là trung điểm \(EF.\)
b) Kẻ \({\rm{A}}H \bot BC\)
Lại có \(EF // BC\) (gt)
\( \Rightarrow \) \(AH \bot EF\)
Mà \(AE = AF\) (chứng minh trên)
Vậy đường cao \(AH\) là đường trung trực của \(EF.\)
Chứng minh tương tự, ta có:
+) \(B\) là trung điểm \(DF\) và \(DF // AC\) nên đường cao kẻ từ đỉnh \(B\) của \(∆ABC\) là đường trung trực của \(DF.\)
+) \(C\) là trung điểm \(DE\) và \(DE // AB\) nên đường cao kẻ từ đỉnh \(C\) của \(∆ABC\) là đường trung trực của \(DE.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 81* trang 51 SBT toán 7 tập 2 timdapan.com"







