Bài 71 trang 50 SBT toán 7 tập 2
Giải bài 71 trang 50 sách bài tập toán 7. Cho hình 15.Chứng minh rằng: CI vuông góc với AB...
Đề bài
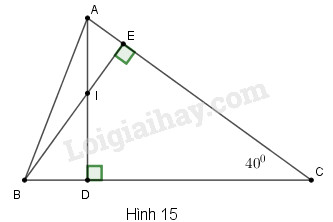
Cho hình 15.
a) Chứng minh rằng: \(CI \bot AB.\)
b) Cho \(\widehat {ACB} = 40^\circ \). Tính \(\widehat {BI{\rm{D}}},\widehat {DIE}\)
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác
+) Tổng hai góc nhọn trong tam giác vuông bằng \(90^0.\)
Lời giải chi tiết
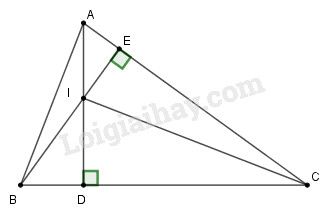
a) Trong \(∆ABC\) ta có hai đường cao \(AD\) và \(BE\) cắt nhau tại \(I\) nên \(I\) là trực tâm của \(∆ABC\)
\( \Rightarrow CI\) là đường cao thứ ba
Vậy \(CI \bot AB\)
b) Trong tam giác vuông \(BEC\) có
\(\widehat {BEC} = 90^\circ \)
\( \Rightarrow \widehat {EBC} + \widehat C = 90^\circ \) (tính chất tam giác vuông)
\( \Rightarrow \widehat {EBC} = 90^\circ - \widehat C \)\(= 90^\circ - 40^\circ = 50^\circ \) hay \(\widehat {IB{\rm{D}}} = 50^\circ \)
Trong tam giác \(IDB\) có \(\widehat {I{\rm{DB}}} = 90^\circ \)
\( \Rightarrow \widehat {IB{\rm{D}}} + \widehat {BI{\rm{D}}} = 90^\circ \) (tính chất tam giác vuông)
\( \Rightarrow \widehat {BI{\rm{D}}} = 90^\circ - \widehat {IB{\rm{D}}}\)\( = 90^\circ - 50^\circ = 40^\circ \)
\(\widehat {BI{\rm{D}}} + \widehat {DIE} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {DIE} = 180^\circ - \widehat {BI{\rm{D}}} \)\(= 180^\circ - 40^\circ = 140^\circ \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 71 trang 50 SBT toán 7 tập 2 timdapan.com"







