Bài 75 trang 51 SBT toán 7 tập 2

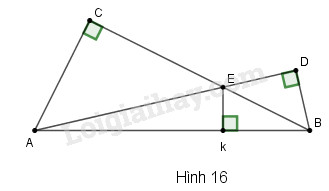
Đề bài

Cho hình 16. Có thể khẳng định rằng các đường thẳng \(AC, BD, KE\) cùng đi qua một điểm hay không? Vì sao? 

Lời giải chi tiết

Trong \(∆AEB\) ta có:

\(AC \bot {\rm{E}}B\) nên \(AC\) là đường cao xuất phát từ đỉnh \(A.\)

\(B{\rm{D}} \bot A{\rm{E}}\) nên \(BD\) là đường cao xuất phát từ đỉnh \(B.\)

\(EK \bot AB\) nên \(EK\) là đường cao xuất phát từ đỉnh \(E.\)

Theo tính chất ba đường cao trong tam giác nên các đường thẳng \(AC, BD\) và \(EK\) cùng đi qua một điểm.