Bài 67 trang 112 SBT toán 9 tập 2
Giải bài 67 trang 112 sách bài tập toán 9. a) Vẽ đường xoắn (h.11) xuất phát từ một hình vuông cạnh 1cm. Nói cách vẽ...
Đề bài
\(a)\) Vẽ đường xoắn \((h.11)\) xuất phát từ một hình vuông cạnh \(1cm.\) Nói cách vẽ.
\(b)\) Tính diện tích hình gạch sọc.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức: Diện tích \(S\) của một hình tròn bán kính \(R\) được tính theo công thức: \(S=\pi.R^2\)
Lời giải chi tiết
\(a)\)
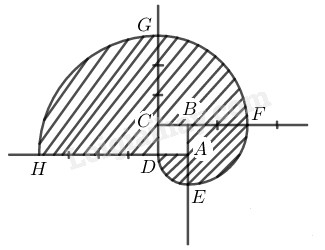
- Vẽ hình vuông \(ABCD\) có cạnh \(1 cm\)
- Vẽ cung đường tròn tâm \(A\) bán kính \(1 cm\) ta được cung \(\overparen{DE}\)
- Vẽ cung đường tròn tâm \(B\) bán kính \(2 cm\) ta được cung \(\overparen{EF}\)
- Vẽ cung đường tròn tâm \(C\) bán kính \(3 cm\) ta được cung \(\overparen{FG}\)
- Vẽ cung đường tròn tâm \(D\) bán kính \(4 cm\) ta được cung \(\overparen{GH}\)
\(b)\) Tính diện tích phần gạch sọc.
Diện tích hình quạt \(DAE = \displaystyle {1 \over 4}\pi {.1^2}\)
Diện tích hình quạt \(EBF = \displaystyle {1 \over 4}\pi {.2^2}\)
Diện tích hình quạt \(FCG = \displaystyle {1 \over 4}\pi {.3^2}\)
Diện tích hình quạt \(GDH =\displaystyle {1 \over 4}\pi {.4^2}\)
Diện tích phần gạch sọc:
\(S = \displaystyle {1 \over 4}\pi \left( {{1^2} + {2^2} + {3^2} + {4^2}} \right) \)\(= \displaystyle{{15} \over 2}(cm^2)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 67 trang 112 SBT toán 9 tập 2 timdapan.com"







