Bài 66 trang 167 SBT toán 9 tập 1

Đề bài

Cho hai đường tròn \((O), (O’)\) tiếp xúc nhau tại \(A\) như trên hình \(78.\) Chứng minh rằng các bán kính \(OB\) và \(O’C\) song song với nhau.

Lời giải chi tiết

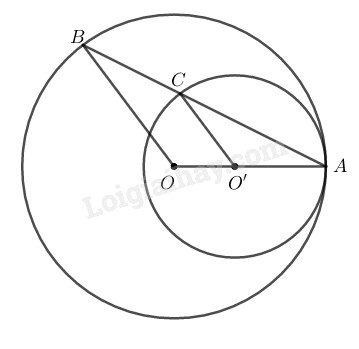
Ta có:    \(OA = OB (= R)\)

Suy ra tam giác \(AOB\) cân tại \(O\)

Hay        \(\widehat {OAB} = \widehat {OBA}\)          \((1)\)

Ta có:    \( O’A = O’C ( = R’ )\)

Suy ra tam giác \(AO’C\) cân tại \(O’\)

Hay       \(\widehat {O'AC} = \widehat {O'CA}\)           \((2)\)

Từ \((1)\) và \((2)\) suy ra: \(\widehat {OBA} = \widehat {O'CA}\)

Suy ra: \(OB // O’C\) ( vì có hai góc ở vị trí đồng vị bằng nhau).