Bài 65 trang 167 SBT toán 9 tập 1
Giải bài 65 trang 167 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B như trên hình 77...
Đề bài
Cho hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B\) như trên hình \(77.\) Biết \(OA = 15cm,\) \(O’A = 13cm,\) \(AB = 24cm.\) Tính độ dài \(OO’.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung.
+) Sử dụng đình lí Py-ta-go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
+) Nếu \(OO' = R + r\) thì đường tròn \((O)\) và đường tròn \((O')\) tiếp xúc ngoài.
Lời giải chi tiết
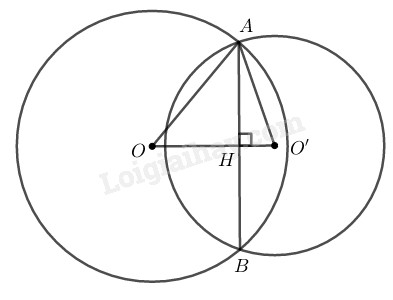
Gọi \(H\) là giao điểm của \(AB\) và \(OO’.\)
Vì \(OO’\) là đường trung trực của \(AB\) nên:
\( OO’ ⊥ AB\) tại \(H.\)
Suy ra: \(HA = HB = \displaystyle{1 \over 2}AB \)\(= \displaystyle{1 \over 2}.24 = 12 (cm)\)
Áp dụng định lí \(Py-ta-go\) vào tam giác vuông \(AOH,\) ta có: \(AO^2=OH^2+AH^2\)
Suy ra: \( OH^2 = OA^2- AH^2 \)\(= 15^2 – 12^2 = 81\)
\(\Rightarrow OH = 9 (cm)\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(AO’H,\) ta có:\(AO'^2=O'H^2+AH^2\)
Suy ra: \( O'H^2 = O'A^2- AH^2 \)\(= 13^2 – 12^2 = 25\)
\(\Rightarrow O'H = 5 (cm)\)
Vậy \(OO’ = OH + O’H \)\(= 9 + 5 = 14 (cm).\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 65 trang 167 SBT toán 9 tập 1 timdapan.com"







