Bài 6 trang 158 Vở bài tập toán 9 tập 2

Đề bài

Từ một điểm \(P\) ở ngoài đường tròn \((O)\), kẻ hai cát tuyến \(PAB\) và \(PCD\) tới đường tròn. Gọi \(Q\) là một điểm nằm trên cung nhỏ \(BD\) (không chứa \(A\) và \(C\)) sao cho sđ\(\overparen{BQ} = 42^\circ \) và sđ \(\overparen{QD}= 38^\circ \). Tính tổng \(\widehat {BPQ} + \widehat {AQC}\) 

Lời giải chi tiết

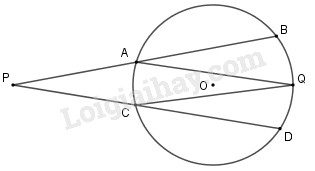
Góc \(BPD\) là góc có đỉnh bên ngoài đường tròn nên

\(\widehat {BPD} = \dfrac{1}{2}\) (sđ\(\overparen{BD}-\) sđ\(\overparen{AC}\))

Góc \(AQC\) là góc nội tiếp chắn cung \(AC\) nên \(\widehat {AQC} = \dfrac{1}{2}\) sđ\(\overparen{AC}\)

Do đó \(\widehat {BPD} + \widehat {AQC} = \dfrac{1}{2}\) (sđ\(\overparen{BD}-\) sđ\(\overparen{AC}\))\( + \dfrac{1}{2}\) sđ\(\overparen{AC}\) \( = \dfrac{1}{2}\) sđ\(\overparen{BD}\)\( = \dfrac{1}{2}\) (sđ \(\overparen{BQ}+\) sđ\(\overparen{QD}\)) \( = \dfrac{1}{2}\left( {42^\circ  + 38^\circ } \right) = 40^\circ \)

Vậy \(\widehat {BPD} + \widehat {AQC} = 40^\circ .\)