Bài 3 trang 157 Vở bài tập toán 9 tập 2

Đề bài

Tam giác \(ABC\) vuông tại \(C\) có \(AC = 15cm\). Đường cao \(CH\) chia \(AB\) thành hai đoạn \(AH\) và \(HB\). Biết \(HB = 16cm\). Tính diện tích tam giác \(ABC\).

Lời giải chi tiết

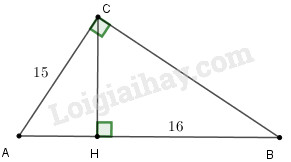
Đặt \(AH = x\left( {x > 0} \right)\) ta có \(AB = AH + HB = x + 16\,\left( {cm} \right)\)

Xét tam giác \(ABC\) vuông tại \(C\) có \(CH\) là đường cao nên ta có \(A{C^2} = AH.AB \Leftrightarrow {15^2} = x\left( {x + 16} \right)\)

\( \Leftrightarrow {x^2} + 16x - 225 = 0 \)\(\Leftrightarrow {x^2} - 9x + 25x - 225 = 0 \)\(\Leftrightarrow x\left( {x - 9} \right) + 25\left( {x - 9} \right) = 0\)

\( \Leftrightarrow \left( {x + 25} \right)\left( {x - 9} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x + 25 = 0\\x - 9 = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x =  - 25\\x = 9\end{array} \right.\)

Vì \(x>0\) nên giá trị \(x=-25\) bị loại.

Vậy \(AH = 9cm\). Trong tam giác vuông AHC có \(CH=\sqrt{AC^2-AH^2}\)\(=\sqrt{15^2-9^2}=12cm\)

Diện tích tam giác \(ABC\) là \({S_{ABC}} = \dfrac{1}{2}AB.CH = \dfrac{1}{2}.(9+16).12\)\( = 150c{m^2}.\)