Giải bài 39 trang 121 sách bài tập toán 9 - Cánh diều tập 1

Đề bài

Cho hình thoi ABCD có cạnh AB = 5cm, đường chéo AC = 8cm. Vẽ các đường tròn (A; 5cm), (C; 3 cm). Đường tròn (C) cắt BC, CD lần lượt tại E, F. Tính tỉ số độ dài của cung nhỏ BD của đường tròn (A) và cung nhỏ EF của đường tròn (C).

Lời giải chi tiết

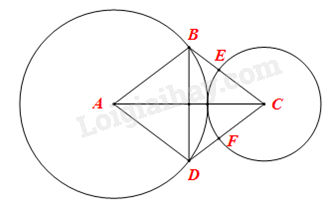
Do ABCD là hình thoi nên \(\widehat {BAD} = \widehat {BCD} = n^\circ \).

Độ dài cung nhỏ BD của (A;5cm) là:

\({l_1} = \frac{{\pi {R_1}n}}{{180}} = \frac{{\pi .5.n}}{{180}} = \frac{{\pi n}}{{36}}\).

Độ dài cung nhỏ EF của (C;3cm) là:

\({l_2} = \frac{{\pi {R_2}n}}{{180}} = \frac{{\pi .3.n}}{{180}} = \frac{{\pi n}}{{60}}\).

Tỉ số độ dài cung nhỏ BD cỉa (A) và cung nhỏ EF của (C) là:

\(\frac{{{l_1}}}{{{l_2}}} = \frac{{\pi n}}{{36}}:\frac{{\pi n}}{{60}} = \frac{5}{3}\).