Giải bài 37 trang 120 sách bài tập toán 9 - Cánh diều tập 1
Hoàn thành số liệu ở bảng sau (làm tròn kết quả đến hàng phần trăm của đơn vị đo đã cho nếu cần, lấy \(\pi \approx 3,14\)):
Đề bài
Hoàn thành số liệu ở bảng sau (làm tròn kết quả đến hàng phần trăm của đơn vị đo đã cho nếu cần, lấy \(\pi \approx 3,14\)):
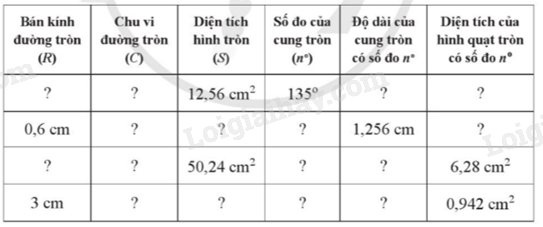
Phương pháp giải - Xem chi tiết
Áp dụng các công thức:
Chu vi hình tròn: \(C = 2\pi R\);
Diện tích hình tròn: \(S = \pi {R^2}\);
Độ dài cung tròn có số đo n⁰: \(l = \frac{{\pi Rn}}{{180}}\);
Diện tích quạt tròn, cung có số đo n⁰: \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết
- Hàng ngang 1: \(S = \pi {R^2}\) hay \(12,56 = \pi {R^2}\), do đó \(R \approx 2\)cm.
Ta có \(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .2.135}}{{180}} \approx 4,71\)cm, \({S_q} = \frac{{\pi {{.2}^2}.135}}{{360}} \approx 4,71\)cm2.
- Hàng ngang 2: \(C = 2\pi R = 2\pi .0,6 \approx 3,768\)cm và \(S = \pi {R^2} = \pi .0,{6^2} \approx 1,1304\)cm2
Ta có \(l = \frac{{\pi Rn}}{{180}}\) hay \(1,256 = \frac{{\pi .0,6.n}}{{180}}\) suy ra \(n \approx 120^\circ \), và \({S_q} = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi .0,{6^2}.120}}{{360}} \approx 0,3768\) cm2
- Hàng ngang 3: \(S = \pi {R^2}\) hay \(50,24 = \pi {R^2}\) do đó \(R \approx 4\)cm và \(C = 2\pi R = 2\pi .4 \approx 25,12\)cm.
Ta có \({S_q} = \frac{{\pi {R^2}n}}{{360}}\) hay \(6,28 = \frac{{\pi {{.4}^2}n}}{{360}}\), do đó \(n \approx 45^\circ \), và \(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .4.45}}{{180}} \approx 3,14\)cm.
- Hàng ngang 4: \(C = 2\pi R = 2\pi .3 \approx 18,84\)cm và \(S = \pi {R^2} = \pi {.3^2} \approx 28,26\) cm2.
Ta có \({S_q} = \frac{{\pi {R^2}n}}{{360}}\) hay \(0,942 = \frac{{\pi {{.3}^2}n}}{{360}}\) do đó \(n \approx 12^\circ \) và \(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .3.12}}{{180}} \approx 0,628\)cm.
Vậy ta có bảng kết quả sau:
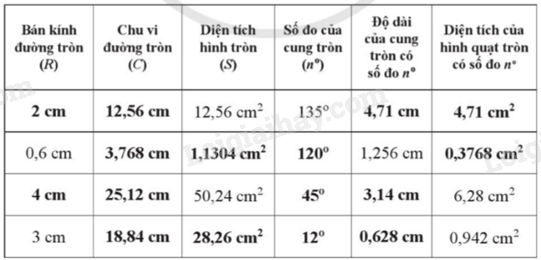
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 37 trang 120 sách bài tập toán 9 - Cánh diều tập 1 timdapan.com"







