Bài 26 trang 127 Vở bài tập toán 7 tập 1

Đề bài

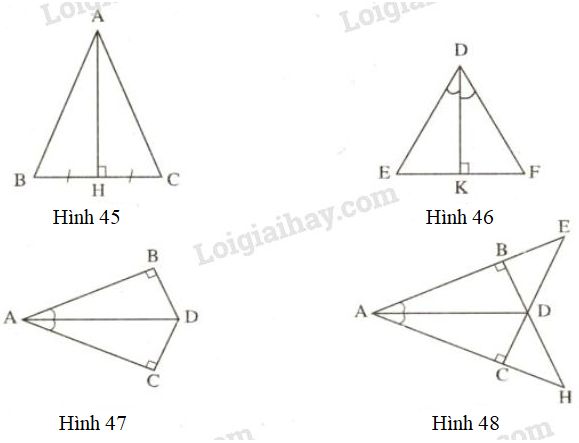
Trên mỗi hình \(45, 46, 47, 48\) các tam giác vuông nào bằng nhau? Vì sao?

Lời giải chi tiết

Trên hình \(45\), ta có \(∆AHB=∆AHC\) (c.g.c) vì \(AH\) là cạnh chung, \(BH=CH\) (gt), \(\widehat{AHB}=\widehat{AHC}=90^o\)

Trên hình \(46\), ta có \(∆DKE=∆DKF\) (g.c.g) vì \(DK\) là cạnh chung, \(\widehat{EDK}=\widehat{FDK}\) (gt), \(\widehat{DKE}=\widehat{DKF}=90^o\)

Trên hình \(47\), ta có \(∆ABD=∆ACD\) (cạnh huyền - góc nhọn) vì \(AD\) là cạnh chung, \(\widehat {DAB} = \widehat {DAC}\,\,\,(gt)\)

Trên hình \(48\), ta có \(∆ABD=∆ACD\) (cạnh huyền - góc nhọn) vì \(AD\) cạnh chung, \(\widehat {DAB} = \widehat {DAC}\,\,\,(gt)\)

\(∆ABD=∆ACD\) suy ra \(  DB=DC,\) \(AB=AC\) (hai cạnh tương ứng )

Ta có \(∆DBE=∆DCH\) (g.c.g) vì \( \widehat {EBD} = \widehat {HCD} = {90^0} \), \(DB=DC\) (chứng minh trên), \(\widehat {BDE} = \widehat {CDH}\) (đối đỉnh)

Ta có  \(∆ABH=∆ACE \) (g.c.g) vì \(\widehat A\) chung, \(AB=AC\) (chứng minh trên), \(\widehat {ABH} = \widehat {ACE} = {90^0}\)