Bài 25 trang 77 Vở bài tập toán 7 tập 2

Đề bài

Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Lời giải chi tiết

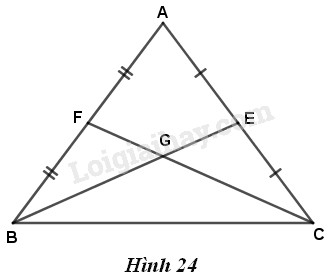
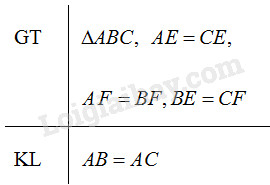
Giả sử \(G\) là giao điểm của \(BE\) và \(CF\) (\(G\) là trọng tâm của tam giác \(ABC\)). Theo tính chất ba đường trung tuyến của tam giác, ta có 

\(BG =2GE\); \(CG =2GF\). 

Mặt khác, theo giả thiết, ta có 

\(GE = \dfrac{1}{3}BE\)\(= \dfrac{1}{3}CF\)\(=GF\). 

Suy ra \(BG = CG.\)

Xét hai tam giác \(BFG\) và \(CEG\). Theo chứng minh trên, ta có \(BG = CG\); \(GE=GF\). Mặt khác, \(\widehat{FGB} = \widehat{EGC}\) (hai góc đối đỉnh)

Vậy \(∆BFG = ∆CEG\) (c.g.c), suy ra \(BF=CE\), do đó \(AB=2BF=2CE=AC\), hay tam giác \(ABC\) cân tại \(A\).