Bài 2.3 phần bài tập bổ sung trang 173 SBT toán 9 tập 1
Giải bài 2.3 trang 173 phần bài tập bổ sung sách bài tập toán 9 Tập 1. Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB...
Đề bài
Cho đường tròn \((O)\) và điểm \(A\) cố định trên đường tròn. Gọi \(xy\) là tiếp tuyến với đường tròn tại \(A.\) Từ một điểm \(M\) nằm trên \(xy,\) vẽ tiếp tuyến \(MB\) với đường tròn. Gọi \(H\) là trực tâm của tam giác \(MAB.\)
\(a)\) Chứng minh rằng ba điểm \(M, H, O\) thẳng hàng.
\(b)\) Tứ giác \(AOBH\) là hình gì \(?\)
\(c)\) Khi \(M\) di chuyển trên \(xy\) thì \(H\) di chuyển trên đường nào \(?\)
Phương pháp giải - Xem chi tiết
\(a)\) Để chứng minh \(M, O, H:\)
- Ta chứng minh \(M, H, O\) cùng nằm trên một tia cố định (trong bài này là tia phân giác của góc \(\widehat {DME}).\)
( Hoặc ta có thể chứng minh \(MO \bot AB,\) suy ra \(MO\) là đường cao của tam giác \(MAB\) mà \(H\) là trực tâm của tam giác này nên \(M,O, H\) thẳng hàng.)
\(b)\) Sử dụng dấu hiệu nhận biết hình thoi (hình bình hành có một cặp cạnh bằng nhau là hình thoi) để chứng minh tứ giác \(AOBH\) là hình thoi.
\(c)\) Liên kết các dữ kiện và các phần đã được chứng minh để tìm ra dược \(H\) cách \(A\) một đoạn không đổi, từ đó tìm được quỹ tích của \(M\) khi chuyển động thì \(H\) cũng chuyển động trên đường tròn tâm \(A,\) bán kính không đổi.
Lời giải chi tiết
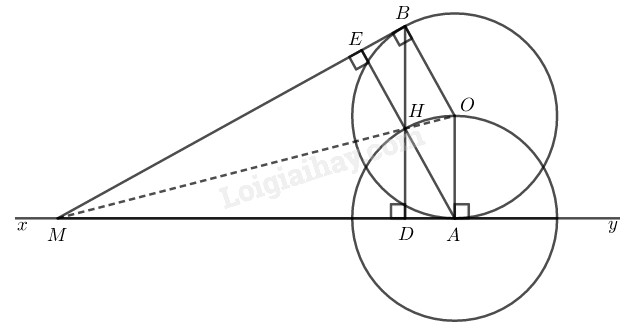
\(a)\) Xét \(∆MBO\) và \(∆MAO\) có:
\(MO\) chung
\(OA=OB\)
Nên \(∆MBO = ∆MAO\) (cạnh huyền – cạnh góc vuông).
Suy ra \(\widehat {BMO} = \widehat {OMA}\) \((1)\)
Gọi \(BD, AE \) là các đường cao của \(∆MAB\).
Xét \(∆MAE\) và \(∆MBD\) có :
\(MA=MB\)
\(\widehat {EMA} = \widehat {DMB}\)
Nên \(∆MAE = ∆MBD\) (cạnh huyền – góc nhọn).
Suy ra \(ME = MD\).
Xét \(∆MHE\) và \(∆MHD\) có:
\(ME = MD\)
\(MH\) chung
\(∆MHE = ∆MHD\) (cạnh huyền – cạnh góc vuông).
Nên \(\widehat {EMH} = \widehat {DMH}\) \((2).\)
Từ \((1)\) và \((2)\) suy ra\(MH\) và \(MO\) đều là tia phân giác của góc \(\widehat {AMB}\) nên \(M, H, O\) thẳng hàng.
\(b)\) Tứ giác \(AOBH\) có
\(BH // OA\) (cùng vuông góc với \(MA\)),
\(AH // OB\) (cùng vuông góc với \(MB\)).
Suy ra tứ giác \(AOBH\) là hình bình hành, mà \(OA = OB\) nên từ giác \(AOBH\) là hình thoi.
\(c)\) Ta có \(HA=OA\) (do \(AOBH\) là hình thoi),
Nên \(H\) cách \(A\) cố định một khoảng bằng \(OA\) không đổi khi \(M\) chuyển động trên \(xy\) thì di chuyển trên đường tròn \((A ; AO).\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.3 phần bài tập bổ sung trang 173 SBT toán 9 tập 1 timdapan.com"







