Bài 2.2 phần bài tập bổ sung trang 173 SBT toán 9 tập 1
Giải bài 2.2 phần bài tập bổ sung trang 173 sách bài tập toán 9. Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, vẽ các tia tiếp tuyến Ax và By với nửa đường tròn. Gọi M là điểm thuộc nửa đường tròn, D là giao điểm của AM và By, C là giao điểm của BM và Ax, E là trung điểm của BD. Chứng minh rằng:...
Đề bài
Cho nửa đường tròn \((O)\) đường kính \(AB.\) Trên nửa mặt phẳng bờ \(AB\) chứa nửa đường tròn, vẽ các tia tiếp tuyến \(Ax\) và \(By\) với nửa đường tròn. Gọi \(M\) là điểm thuộc nửa đường tròn, \(D\) là giao điểm của \(AM\) và \(By,\) \(C\) là giao điểm của \(BM\) và \(Ax,\) \(E\) là trung điểm của BD. Chứng minh rằng:
\(a)\) \(AC.BD = AB^2;\)
\(b)\) \(ME\) là tiếp tuyến của nửa đường tròn.
Phương pháp giải - Xem chi tiết
\(a)\) Sử dụng định lí về hai tam giác đồng dạng để thiết lập tỉ số giữa các cạnh, từ đó chứng minh được biểu thức đề bài đưa ra.
\(b)\) Theo tính chất của tiếp tuyến, ta phải chứng minh được \(ME ⊥ OM\) tại \(M.\)
Sử dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta tìm các góc bằng nhau, thiết lập mối liên hệ giữa chúng.
Lời giải chi tiết
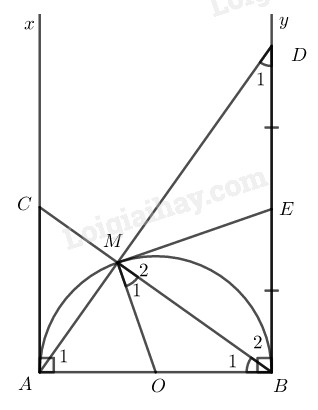
\(a)\) \(\widehat {{B_1}} = \widehat {{D_1}}\) ( cùng phụ với \(\widehat {{A_1}}\)).
Xét \(∆ABC\) và \(∆BDA\) có:
\(\widehat {{B_1}} = \widehat {{D_1}}\)
\(\widehat A = \widehat B = 90^\circ \)
\(∆ABC\) đồng dạng với \(∆BDA \;\;(g.g)\) suy ra:
\(\displaystyle{{AB} \over {BD}} = {{AC} \over {AB}}\), do đó \(AC . BD = AB^2\)
\(b)\) Áp dụng định lí trong tam giác vuông đường trung tuyến ứng với canh huyền thì bằng nửa cạnh huyền.
Ta có trong \(∆MBD\) có \(ED = EM = EB\)
\(∆EBM\) cân nên \(\widehat {{M_2}} = \widehat {{B_2}}\)\((1)\)
\(∆MOB\) cân tại \(O\) nên \(\widehat {{M_1}} = \widehat {{B_1}}\) \((2)\)
Từ \((1)\) và \((2)\) suy ra
\(\widehat {{M_1}} + \widehat {{M_2}}\) = \(\widehat {{B_1}} + \widehat {{B_2}}\) = \(90^\circ \),
tức là \(ME ⊥ OM\) tại \(M.\)
Vậy \(ME\) là tiếp tuyến của nửa đường tròn.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.2 phần bài tập bổ sung trang 173 SBT toán 9 tập 1 timdapan.com"







