Bài 2.1, 2.2, 2.3 phần bài tập bổ sung trang 39 SBT toán 7 tập 2

Bài 2.1

Cho đường thẳng \(d\) và điểm \(A\) không thuộc \(d.\) Trong các khẳng định sau đây, khẳng định nào đúng, khẳng định nào sai? 

(A) Có duy nhất một đường vuông góc kẻ từ điểm \(A\) đến đường thẳng \(d.\)

(B)  Có duy nhất một đường xiên kẻ từ điểm \(A\) đến đường thẳng \(d.\)

(C)  Có vô số đường vuông góc kẻ từ điểm \(A\) đến đường thẳng \(d.\)

(D) Có vô số đường xiên kẻ từ điểm \(A\) đến đường thẳng \(d.\)

Hãy vẽ hình minh họa cho các khẳng định đúng.

Phương pháp giải:

Sử dụng: Từ một điểm nằm ngoài một đường thẳng có duy nhất một đường vuông góc và vô số đường xiên đến đường thẳng đó.

Lời giải chi tiết:

Ta có: Từ một điểm nằm ngoài một đường thẳng có duy nhất một đường vuông góc và vô số đường xiên đến đường thẳng đó.

Suy ra các đáp án (A) và (D) đúng, (B) và (C) sai.

Hình minh họa:

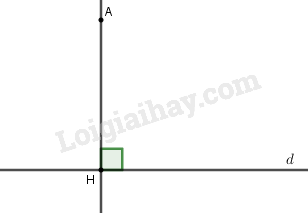
(A) Có duy nhất một đường vuông góc kẻ từ điểm \(A\) đến đường thẳng \(d.\)

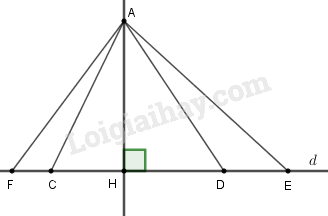
(D) Có vô số đường xiên kẻ từ điểm \(A\) đến đường thẳng \(d.\)

Trong hình trên thì các đường \(AF;AC;AD;AE\) đều là các đường xiên kẻ từ \(A\) đến đường thẳng \(d\) và có vô số đường xiên như thế. 

Bài 2.2

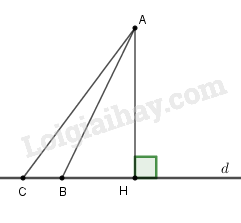
Qua điểm \(A\) không thuộc đường thẳng \(d,\) kẻ đường vuông góc \(AH\) và các đường xiên \(AB, AC\) đến đường thẳng \( d\) (\(H, B, C\) đều thuộc \(d).\) Biết rằng \(HB < HC.\) Hãy chọn khẳng định đúng trong các khẳng định sau:

(A) \(AB > AC \)              (B) \(AB = AC\)

(C) \(AB < AC\)               (D) \(AH > AB\)

Phương pháp giải:

Sử dụng: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: Đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn

Lời giải chi tiết:

Ta có các đường xiên \(AB,AC\) lần lượt có hình chiếu trên đường thẳng \(d\) là \(HB,HC\)

Theo định lý so sánh giữa hình chiếu và hình xiên ta có: \(HB < HC \Rightarrow AB < AC.\) 

Chọn (C)

Bài 2.3

a) Hai tam giác \(ABC, A’B’C’  \)vuông tại \(A\) và \(A’\) có \(AB = A’B’, AC > A’C’.\) Không sử dụng định lý Pytago, chứng minh rằng \(BC > B’C’.\)

b) Hai tam giác \(ABC, A’B’C’\) vuông tại \(A \) và \(A’\) có \(AB = A’B’, BC > B’C’.\) Không sử dụng định lý Pytago, chứng minh rằng \(AC > A’C’.\) 

Phương pháp giải:

Sử dụng: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó;

a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn

b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn

Và sử dụng tính chất hai tam giác bằng nhau. 

Lời giải chi tiết:

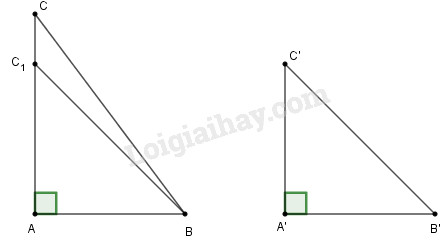
a) Do \(AC > A’C’\) nên lấy được điểm \({C_1}\) trên cạnh \(AC\) sao cho \({\rm{A}}{C_1} = A'C'\).

Xét hai tam giác vuông \(ABC_1\) và \(A'B'C'\) có \(AB=A'B';\,AC_1=A'C'\)

Suy ra tam giác vuông \(AB{C_1}\) bằng tam giác vuông \(A’B’C’,\) do đó \(B'C' = B{C_1}\).

Mặt khác hai đường xiên \(BC\) và \(B{C_1}\) kẻ từ B đến đường thẳng \(AC\) lần lượt có hình chiếu trên \(AC\) là \(AC \) và \({\rm{A}}{C_1}\). Vì \({\rm{A}}C > A{C_1}\) nên \(BC > B{C_1}\) (quan hệ giữa đường xiên và hình chiếu) Suy ra \(BC > B’C’.\)

b) Dùng phản chứng:

- Giả sử \(AC < A’C’.\) Khi đó theo chứng minh câu a) ta có \(BC < B’C’.\) Điều này không đúng với giả thiết \(BC > B’C’.\)

- Giả sử \(AC = A’C’.\) Khi đó ta có \(∆ABC = ∆A’B’C’ (c.g.c).\) Suy ra  \(BC = B’C’.\)

Điều này cũng không đúng với giả thiết \(BC > B’C’.\)

Vậy ta phải có \(AC > A’C’.\)

Chú ý: 

Nếu sử dụng định lý Pytago thì có thể giải bài toán như sau:

Trong tam giác vuông \(ABC \) có \(BC^2= AB^2+ AC^2\) (1)

Trong tam giác vuông \(A'B'C' \) có \(B'C'^2= A'B'^2+ A'C'^2\) (2)

Theo giả thiết \(AB = A'B'\) nên từ (1) và (2) ta có:

- Nếu \(AC > A'C' \) thì \(AC^2 > A'C'^2,\) suy ra \(BC^2 > B'C'^2\) hay \(BC > B'C'\)

- Nếu \(BC > B'C'\) thì \(BC^2 > B'C'^2,\) suy ra \(AC^2 > A'C'^2\) hay \(AC > A'C'.\)