Bài 16 trang 38 SBT toán 7 tập 2
Giải bài 16 trang 38 sách bài tập toán 7. Cho tam giác ABC cân tại A, điểm D nằm giữa B và C. Chứng minh rằng độ dài AD nhỏ hơn cạnh bên của tam giác ABC.
Đề bài
Cho tam giác \(ABC\) cân tại \(A, \) điểm \(D\) nằm giữa \(B\) và \(C.\) Chứng minh rằng độ dài \(AD\) nhỏ hơn cạnh bên của tam giác \(ABC.\)
Phương pháp giải - Xem chi tiết
Kẻ \(AH \bot BC\)
Sử dụng:
+) Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
+) Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: Đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn
Lời giải chi tiết
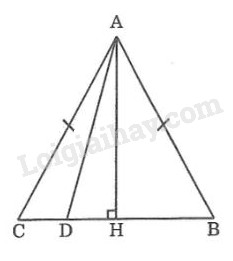
Kẻ \(AH \bot BC\)
+) Trường hợp 1: Nếu \(H\) trùng với \(D\)
Ta có \(AH < AC\) (đường vuông góc ngắn hơn đường xiên)
Suy ra: \(AD < AC\)
+) Trường hợp 2: Điểm \(H\) không trùng \(D\)
Giả sử \(D\) nằm giữa \(H\) và \(C\)
Khi đó \(HD < HC\) mà \(HD,HC\) lần lượt là hình chiếu của các đường xiên \(AD,AC\) xuống đường thẳng \(BC\)
\( \Rightarrow AD < AC\) (hình chiếu nhỏ hơn thì có đường xiên nhỏ hơn)
Vậy \(AD\) nhỏ hơn cạnh bên của tam giác cân \(ABC.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 16 trang 38 SBT toán 7 tập 2 timdapan.com"







