Bài 14 trang 38 SBT toán 7 tập 2
Giải bài 14 trang 38 sách bài tập toán 7. Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BD. So sánh AC với tổng AE + CF.
Đề bài
Cho tam giác \(ABC,\) điểm \(D\) nằm giữa \(A\) và \(C\) (\(BD\) không vuông góc với \(AC).\) Gọi \(E \) và \(F\) là chân các đường vuông góc kẻ từ \(A\) và \(C\) đến đường thẳng \(BD.\) So sánh \(AC\) với tổng \(AE + CF.\)
Phương pháp giải - Xem chi tiết
Sử dụng: Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Lời giải chi tiết
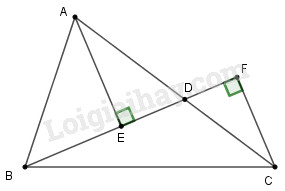
Vì \(AE \bot BD\) nên AE là đường vuông góc hạ từ đỉnh A xuống đường thẳng BD và AD là đường xiên.
Nên \(AE < AD\) (1) (quan hệ giữa đường xiên và đường vuông góc)
Vì \(CF \bot BD\) nên CF là đường vuông góc hạ từ đỉnh A xuống đường thẳng BD và CD là đường xiên.
Nên \(CF < CD\) (2) (quan hệ giữa đường xiên và đường vuông góc)
Cộng từng vế (1) và (2) ta có:
\(AE + CF < AD + CD\)
Mà \(D\) nằm giữa \(A\) và \(C\) nên \(AD + CD = AC\)
Vậy \(AE + CF < AC \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 14 trang 38 SBT toán 7 tập 2 timdapan.com"







