Bài 13 trang 38 SBT toán 7 tập 2
Giải bài 13 trang 38 sách bài tập toán 7. Cho tam giác ABC cân tại A có AB = AC = 10cm, BC = 12cm. Vẽ cung tròn tâm A có bán kính 9cm. Cung đó có cắt đường thẳng BC hay không, có cắt cạnh BC hay không? Vì sao?
Đề bài
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 10cm, BC = 12cm.\) Vẽ cung tròn tâm \(A\) có bán kính \(9cm.\) Cung đó có cắt đường thẳng \(BC\) hay không, có cắt cạnh \(BC\) hay không? Vì sao?
Phương pháp giải - Xem chi tiết
+) Kẻ \(AH \bot BC\), tính \(AH\) theo định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
+) Sử dụng:
Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: Đường xiên nào lớn hơn thì có hình chiếu lớn hơn
Lời giải chi tiết
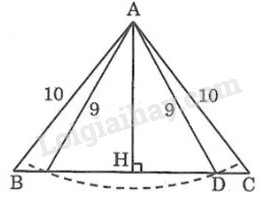
Kẻ \(AH \bot BC\)
Suy ra \(\widehat {AHB} = \widehat {AHC} = 90^\circ \)
Và \(\displaystyle HB = HC = {{BC} \over 2} = 6\left( {cm} \right)\) (do tam giác \(ABC\) cân tại \(A\) nên đường cao \(AH\) cũng là đường trung tuyến)
Xét tam giác \(AHB\) vuông tại \(H,\) theo định lý Pytago ta có:
\(\eqalign{
& A{B^2} = A{H^2} + H{B^2} \cr
& A{H^2} = A{B^2} - H{B^2} \cr
& A{H^2} = {10^2} - {6^2} = 64 \cr
& \Rightarrow AH = 8\left( {cm} \right) \,(do\,AH > 0) \cr} \)
Do bán kính cung tròn \(9 (cm) > 8 (cm)\) nên cung tròn tâm \(A\) bán kính \(9 cm\) cắt đường thẳng \(BC.\)
Gọi \(D\) là giao điểm của cung tròn tâm \(A\) bán kính \(9 cm\) với \(BC\), ta có đường xiên \(AD < AC \,(9cm<10cm)\) nên hình chiếu \(HD < HC\) (quan hệ giữa đường xiên và hình chiếu), do đó \(D\) nằm giữa \(H\) và \(C.\)
Vậy cung tròn tâm \(A\) bán kính \(9cm\) cắt cạnh \(BC.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 13 trang 38 SBT toán 7 tập 2 timdapan.com"







