Bài 1.32 trang 37 SBT hình học 11
Giải bài 1.32 trang 37 sách bài tập hình học 11. Cho hình bình hành ABCD có AB cố định, đường chéo AC có độ dài bằng m không đổi. Chứng minh rằng khi C thay đổi, tập hợp các điểm D thuộc một đường tròn cố định.
Đề bài
Cho hình bình hành \(ABCD\) có \(AB\) cố định, đường chéo \(AC\) có độ dài bằng \(m\) không đổi. Chứng minh rằng khi \(C\) thay đổi, tập hợp các điểm \(D\) thuộc một đường tròn cố định.
Phương pháp giải - Xem chi tiết
Tìm quỹ tích điểm \(C\) và sử dụng tính chất của phép tịnh tiến để suy ra quỹ tích điểm \(D\).
Lời giải chi tiết
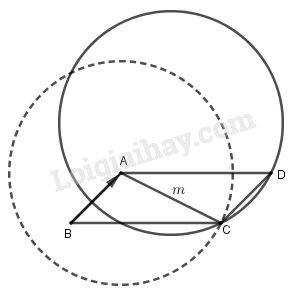
Dễ thấy \(\overrightarrow {CD} = \overrightarrow {AB} \) và \(A,B\) cố định nên \(D = {T_{\overrightarrow {BA} }}\left( C \right)\).
Do \(C\) chạy trên đường tròn \(\left( C \right)\) tâm \(A\) bán kính \(m\), trừ ra giao điểm của \(\left( C \right)\) với đường thẳng \(AB\), nên \(D\) thuộc đường tròn là ảnh của đường tròn nói trên qua phép tịnh tiến theo vectơ \(\overrightarrow {BA} \).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.32 trang 37 SBT hình học 11 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.32 trang 37 SBT hình học 11 timdapan.com"







