Đề số 8 - Đề kiểm tra học kì 1 - Toán lớp 4

Đề bài

Câu 1. Khoanh vào chữ đặt trước câu trả lời đúng :

a) Cho 6 chữ số 1, 2, 5, 6, 9, 0. Hãy viết số bé nhất gồm 6 chữ số đã cho.

A. 012 569                            B. 125 690                           C. 102 569.

b) Giá trị của chữ số 5 trong số bé nhất có 6 chữ số khác nhau là :

A. 5                                      B. 50                                   C. 500.

Câu 2. Viết số thích hợp vào chỗ chấm :

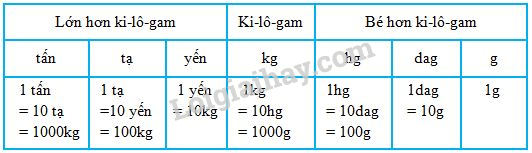
2 tạ 3 yến 5kg = … kg ;                               5 yến 6kg = …… kg ;

3 tấn 5 tạ = …… kg ;                                   300 yến = …… tấn ;

1200kg = …… tạ ;                                       80 000kg = …… tấn.

Câu 3. Khoanh vào chữ đặt trước câu trả lời đúng :

Bảng sau ghi tên vận động viên và thời gian chạy trên cùng một quãng đường của mỗi người :

Khuê	Văn	Tú	Quân
13 phút	\(\dfrac{1}{5}\) giờ	700 giây	12 phút 45 giây

Người chạy nhanh nhất là :

A. Khuê                                          B. Văn

C. Tú                                              D. Quân.

Câu 4. Đúng ghi Đ, sai ghi S :

Điền dấu ( >, <, = ) thích hợp vào chỗ chấm :

a) 2 tấn 10kg ….. 20 tạ 1kg.

    2 tấn 10kg > 2 tạ 1kg  ☐

    2 tấn 10kg = 2 tạ 1kg  ☐

    2 tấn 10kg < 2 tạ 1kg  ☐

b) \(\dfrac{1}{4}\) thế kỉ … 300 tháng

    \(\dfrac{1}{4}\)thế kỉ > 300 tháng  ☐

    \(\dfrac{1}{4}\) thế kỉ = 300 tháng  ☐

    \(\dfrac{1}{4}\) thế kỉ < 300 tháng  ☐

Câu 5. Viết số thích hợp vào chỗ chấm :

 a)  40000 giây = … giờ … phút … giây

 b)  1 ngày = … giây.

Câu 6. Một chiếc cầu dài \(800m\) có biển cấm ô tô chạy quá \(10km\) một giờ. Một người lái xe đã cho ô tô chạy qua cầu hết \(\dfrac{1}{{12}}\) giờ. Hỏi người đó có tôn trọng luật giao thông không ?

Câu 7. Ba ô tô chở hàng. Ô tô thứ nhất chở được \(4\) tạ \(5\) yến, ô tô thứ hai chở bằng \(\dfrac{1}{5}\) lượng hàng của ô tô thứ nhất, nhưng bằng \(\dfrac{1}{4}\) khối lượng hàng của ô tô thứ ba. Hỏi cả ba ô tô chở được bao nhiêu ki-lô-gam hàng ?

Câu 8. Khi viết các số tự nhiên liên tiếp từ 1 đến 2009 thì phải viết tất cả bao nhiêu chữ số ?

---

Lời giải

Câu 1.

Phương pháp:

a) Dựa vào tính chất của dãy số tự nhiên để viết số thỏa mãn yêu cầu bài toán.

b) Viết số bé nhất có 6 chữ số khác nhau rồi xác định hàng của chữ số 5, sau đó viết giá trị của chữ số 5.

Cách giải:

a) Số bé nhất gồm 6 chữ số 1, 2, 5, 6, 9, 0 là 102 569.

    Chọn C.

b) Số bé nhất có 6 chữ số khác nhau là 102 345.

    Trong số 102 345, chữ số 5 thuộc hàng đơn vị nên có giá trị là 5.

    Chọn A.

Câu 2. 

Phương pháp:

 Dựa vào bảng đơn vị đo khối lượng: 

Cách giải:

+) 2 tạ 3 yến 5kg = 2 tạ + 3 yến + 5kg = 200kg + 30kg + 5kg = 235 kg;

+) 5 yến 6kg = 5 yến + 6kg = 50kg + 6kg = 56kg;

+) 3 tấn 5 tạ = 3 tấn + 5 tạ  = 3000kg + 500kg = 3500kg;

+) 1 tấn = 100 yến. Mà 300 : 100 = 3 nên 300 yến = 3 tấn.

+) 1 tạ = 100kg. Mà 1200 : 100 = 12 nên 1200kg = 12 tạ;

+) 1 tấn = 1000kg. Mà 80 000 : 1000 = 80 nên 80 000kg = 80 tấn.

Câu 3.

Phương pháp:

Đổi các số đo về cùng một đơn vị rồi so sánh kết quả với nhau. Người chạy nhanh nhất là người chạy với thời gian ít nhất.

Cách giải:

Ta có:

+) 13 phút = 60 giây × 13 = 780 giây;

+) \(\dfrac{1}{5}\) giờ = 60 phút \(\times \dfrac{1}{5}\) = 12 phút = 720 giây ;

+) 12 phút 45 giây = 12 phút + 45 giây = 720 giây + 45 giây = 765 giây

Mà: 700 giây < 720 giây < 765 giây < 780 giây

Vậy người chạy nhanh nhất là Tú.

Chọn C. 

Câu 4. 

Phương pháp:

Đổi các số đo về cùng một đơn vị đo rồi cùng so sánh với nhau.

Cách giải:

a) Ta có:  2 tấn 10kg = 2010kg  ;    20 tạ 1kg = 2001kg

     Mà:    2010kg > 2001kg

    Vậy:   2 tấn 10kg > 2 tạ 1kg 

    Ta có kết quả lần lượt là:   Đ ;          S ;           S.

b) Ta có: 1 thế kỉ = 100 năm nên \(\dfrac{1}{4}\) thế kỉ = 100 năm \(\times\,\dfrac{1}{4}\) = 25 năm.

    Lại có 1 năm = 12 tháng nên 25 năm = 12 tháng × 25 = 300 tháng.

    Vậy: \(\dfrac{1}{4}\) thế kỉ = 300 tháng

    Ta có kết quả lần lượt là:   S ;          Đ ;           S.

Câu 5.

Phương pháp:

Dựa vào cách chuyển đổi: 

1 giờ = 60 phút  ;              1 phút = 60 giây  ;                  1 ngày = 24 giờ.

Cách giải:

a) Ta có: 4000 : 60 = 66 dư 40 nên 4000 giây = 66 phút 40 giây.

    Lại có: 66 phút = 1 giờ 6 phút.

    Vậy: 4000 giây = 1 giờ 6 phút 40 giây.

b) Ta có: 1 giờ = 60 giây × 60 = 3600 giây.

    Mà 1 ngày = 24 giờ nên 1 ngày = 3600 giây × 24 = 86 400 giây.

    Vậy: 1 ngày = 86 400 giây.

Câu 6.

Phương pháp:

- Đổi: \(\dfrac{1}{{12}}\) giờ \(= 5\) phút  ; \(1\) giờ \(=60\) phút.

- Tính số mét đường đi được trong \(1\) phút ta lấy \(800\) chia cho \(5\).

- Tính số mét đường đi được trong \(1\) giờ ta lấy số mét đường đi được trong \(1\) phút nhân với \(60\).

- So sánh số đo vừa tìm được với \(10km\), nếu lớn hơn \(10km\) thì vi phạm luật giao thông.

Cách giải:

\(\dfrac{1}{{12}}\) giờ \(= 5\) phút  ; \(1\) giờ \(=60\) phút.

Trong \(1\) phút người đó lái ô tô chạy được số mét là :

                     \(800 : 5  = 160\;(m)\) 

Trong \(1\) giờ người đó lái ô tô chạy được số ki-lô-mét là :

                     \(800 : 5 × 60 = 9600\;(m)\) 

                     \(9600m = 9km \;600m\)

Vì \(9km \;600m < 10km\) nên người đó tôn trọng luật giao thông.

Câu 7.

Phương pháp:

- Đổi : \(4\) tạ \(5\) yến \(= 450kg.\)

- Tính số hàng ô tô thứ hai chở \( =\) số hàng ô tô thứ nhất chở \(:\,5\).

- Tính số hàng ô tô thứ ba chở \( =\) số hàng ô tô thứ hai chở \(\times \,5\).

- Tính số hàng ba ô tô chở \( =\) số hàng ô tô thứ nhất chở \(+\) số hàng ô tô thứ hai chở \(+\) số hàng ô tô thứ ba chở.

Cách giải:

Đổi: \(4\) tạ \(5\) yến \(= 450kg.\)

Ô tô thứ hai chở được số ki-lô-gam hàng là:

               \(450 : 5  = 90\;(kg)\)

Ô tô thứ ba chở được số ki-lô-gam hàng là:

               \(90 × 4 = 360\;(kg)\)

Cả 3 ô tô chở được số ki-lô-gam hàng là:

               \(450 + 90 + 360 = 900\;(kg)\) 

                                Đáp số : \(900kg\).

Câu 8.

Phương pháp:

- Tìm số các số có \(1\) chữ số, \(2\) chữ số, \(3\) chữ số theo công thức tìm số số hạng của dãy số cách đều:

         Số số hạng \(=\;(\)số cuối \(-\) số đầu\()\;:\) khoảng cách giữa hai số \(+1\). 

- Tìm số chữ số cần dùng \(=\) \(1 \times\) số các số có \(1\) chữ số \(+\) \(2 \times\) số các số có \(2\) chữ số \(+\) \(3 \times\) số các số có \(3\) chữ số \(+\) \(4 \times\) số các số có \(4\) chữ số.

Cách giải:

Dãy các số có \(1\) chữ số là: \(1;\;2;\;3;\;...\;8;\;9\).

Số các số có \(1\) chữ số là

              \((9 \;– 1):1 + 1 = 9\)

Dãy các số có \(2\) chữ số là: \(10;\;11;\;12;\;...\;98;\;99\).

Số các số có \(2\) chữ số là

              \((99 \;– 10):1 + 1 = 90\)

Dãy các số có \(3\) chữ số là: \(101;\;102;\;103;\;...\;998;\;999\).

Số các số có \(3\) chữ số là

              \((999 \;– 100):1 + 1 = 900\)

Dãy các số có \(4\) chữ số là: \(1000;\;1002;\;1003;\;...\;2008;\;2009\).

Số các số có \(4\) chữ số là

              \((2009 \;– 1000):1 + 1 = 1010\)

Số lượng chữ số để viết dãy số tự nhiên liên tiếp từ \(1\) đến \(2009\) là:

              \(1 × 9 + 2 × 90 + 3× 900 \)\(  + 4 × 1010 = 6929\) (chữ số ).

                                          Đáp số : \(6929\) chữ số.