Đề số 18 - Đề kiểm tra học kì 1 - Toán lớp 4

Đáp án và lời giải chi tiết Đề số 18 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán lớp 4

Đề bài

Câu 1. Đúng ghi Đ, sai ghi S:

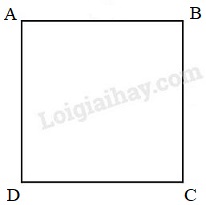
Hình vẽ bên có:

a) 3 góc vuông, 3 góc tù. ☐

b) 2 góc nhọn, 2 góc tù. ☐

c) 2 cặp cạnh song song với nhau. ☐

d) 3 cặp cạnh song song với nhau. ☐

Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng :

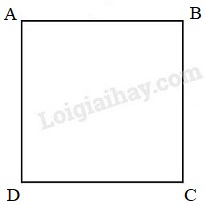
A. 2 đường chéo của hình vuông không bằng nhau.

B. 2 đường chéo của hình vuông bằng nhau.

C. 2 đường chéo của hình vuông không vuông góc với nhau.

D. 2 đường chéo của hình vuông vuông góc với nhau.

Câu 3. Đúng ghi Đ, sai ghi S :

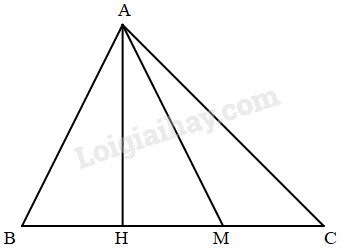
Trong hình vẽ bên trên:

a) AM là chiều cao của tam giác AMC. ☐

b) AH là chiều cao của tam giác ABC. ☐

c) AM là chiều cao của tam giác ABC. ☐

d) AH là chiều cao của tam giác AMC. ☐

Câu 4. Khoanh vào chữ đặt trước câu trả lời đúng :

Tổng của hai số bằng hiệu của hai số đó khi :

A. Hai số đều là số chẵn. B. Hai số đều là số 0.

C. Hai số đều là số lẻ. D. Một trong hai số bằng 0.

Câu 5. Cho 4 chữ số 0, 1, 2, 3. Hãy lập tất cả các số có 3 chữ số khác nhau rồi tính tổng tất cả các số đó bằng cách nhanh nhất.

Câu 6. Cho hình vuông ABCD, MN song song với hai cạnh AB và CD. Trên MN lấy điểm I, từ I vẽ đường thẳng song song với hai cạnh AD và BC, cắt AB tại E và CD tại F. Nối E với M và N, nối F với M và N. Ghi tên các hình chữ nhật và hình tam giác có trong hình vẽ.

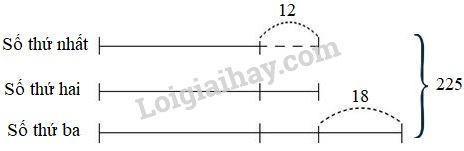
Câu 7. Tổng của 3 số 225. Tìm 3 số đó, biết số thứ nhất kém số thứ hai 12. Số thứ hai kém số thứ ba 18.

Lời giải

Câu 1.

Phương pháp:

Quan sát hình vẽ để tìm các góc có trong hình vẽ, tìm các cặp cạnh song song với nhau.

Cách giải:

Trong hình đã cho có :

+ 4 góc vuông, đó là góc A, góc B, góc C, góc D.

+ 2 cặp cạnh song song là: AB và CD, AD và BC.

Vậy ta có: kết quả như sau:

a) S b) S c) Đ d) S

Câu 2.

Phương pháp:

Vẽ hình vuông bất kì, sau đó có thể dùng thước kẻ và ê kê để kiểm tra độ dài và tính vuông góc của hai đường chéo.

Cách giải:

Dùng thước kẻ kiểm tra ta thấy AC = BD.

Dùng ê ke kiểm tra ta thấy AC vuông góc với BB.

Vậy 2 đường chéo của hình vuông bằng nhau và vuông góc với nhau.

Chọn B và D.

Câu 3.

Phương pháp:

Quan sát hình vẽ để xác định chiều cao của các tam giác. Chiều cao của 1 tam giác là đoạn thẳng vuông góc với cạnh đáy của tam giác đó.

Cách giải:

Trong hình vẽ đã có:

+ AH là chiều cao của tam giác ABC.

+ AH là chiều cao của tam giác AMC.

Vậy ta có: kết quả như sau:

a) S b) Đ c) S d) Đ

Câu 4.

Phương pháp:

Tổng của hai số bằng hiệu của hai số đó khi một trong hai số bằng 0.

Có thể lấy ví dụ để hiểu rõ hơn.

Cách giải:

Tổng của hai số bằng hiệu của hai số đó khi một trong hai số bằng 0.

Ví dụ: 5 và 0; 0 và 10; ...

Chọn D.

Câu 5.

Phương pháp:

Các số có 3 chữ số được viết từ từ bốn chữ số sau: 0, 1, 2, 3 thì phải có chữ số hàng trăm khác 0. Do đó, chữ số hàng trăm là là 1, 2 hoặc 3.

Chữ số hàng chục có thể là 1 trong 4 chữ số 0, 1, 2, 3 (khác với chữ số hàng trăm).

Chữ số hàng đơn vị có thể là 1 trong 4 chữ số 0, 1, 2, 3 (khác với chữ số hàng trăm và hàng chục).

Cách giải:

Từ bốn chữ số 0, 1, 2, 3 ta viết được các số có 3 chữ số khác nhau là:

- 102, 103, 120, 130, 123, 132

- 201, 203, 210, 213, 230, 231

- 301, 302, 310, 312, 320, 321

Nhận xét : Trừ chữ số 0 các chữ số còn lại đều đứng ở hàng trăm 6 lần, hàng chục 4 lần, hàng đơn vị 4 lần.

Tổng của 18 số đó là :

\(100 × 6 × (1 + 2 + 3)\)\( + 10 × 4 × (1 + 2 + 3)\)\( + 1 × 4 × (1 + 2 + 3)\)

\(= 600 × 6 + 40 × 6 + 4 × 6\)

\(= ( 600 + 40 +4 ) ×6\)

\(= 644 × 6 = 3864.\)

Câu 6.

Phương pháp:

Vẽ hình theo đề bài rồi liệt kê tên của các hình chữ nhật, hình tam giác có trong hình vẽ

Cách giải:

Theo đề bài ta có hình vẽ như sau:

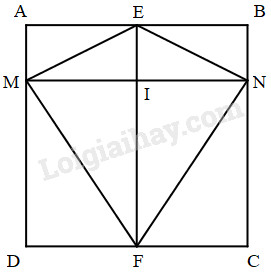
Hình trên có:

Có 8 hình chữ nhật: AEIM, EBNI, MIFD, INCF, ABNM, MNCD, AEFD, EBCF.

Có 12 hình tam giác là: AEM, EBN, NCF, MDF, EIM, ENI, IFN, MIF, MEF, EFN, MEN, MNF.

Câu 7.

Phương pháp:

Vẽ sơ đồ biểu diễn ba số. Từ sơ đồ ta thấy \(3\) lần số thứ hai là \(225 +12 - 18\). Từ đó tìm được số thứ hai. Tìm số thứ nhất, số thứ ba dựa vào số thứ hai.

Cách giải:

Ta có sơ đồ: