Đề kiểm tra 45 phút ( 1 tiết) - Đề số 1 - Chương 1 - Hình học 11

Đề bài

Câu 1: Có bao nhiêu phép tịnh tiến một đường tròn cho trước thành chính nó?

A.Không có                           

B. Một                              

C. Hai                        

D. Vô số

Câu 2: Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vectơ \(\vec v = ( - 3;2)\) biến điểm A ( 1;3) thành điểm nào trong các điểm sau:

A.(-3;2)                                  

B. (1;3)                             

C. (-2;5)                     

 D. (2;-5)

Câu 3: Trong mặt phẳng với hệ trục Oxy, cho phép tịnh tiến theo vectơ \(\vec v = (1;1)\), phép tịnh tiến theo \(\vec v\)biến d: x -1= 0 thành đường thẳng \(d'\). Khi đó phương trình của \(d'\)là:

A.x – 1 = 0                            

B. x – 2 = 0                       

C. x – y -2 = 0           

D. y – 2 =0

Câu 4: Trong mặt phẳng Oxy, ảnh của đường tròn : \({(x - 2)^2} + {(y - 1)^2} = 16\)qua phép tịnh tiến theo vectơ \(\vec v = (1;3)\) là đường tròn có phương trình :

A. \({(x - 2)^2} + {(y - 1)^2} = 16\)   

B. \({(x + 2)^2} + {(y + 1)^2} = 16\)

C. \({(x - 3)^2} + {(y - 4)^2} = 16\)         

D. \({(x + 3)^2} + {(y + 4)^2} = 16\)

Câu 5: Cho tam giác ABC đều. Hỏi tam giác ABC đều có bao nhiêu trục đối xứng:

A. Không có trục đối xứng                                               

B. Có 1 trục đối xứng

C. Có 2 trục đối xứng                                                      

D. Có 3 trục đối xứng

Câu 6: Trong mặt phẳng tọa độ Oxy cho parabol (P): \({y^2} =  - 12x\). Hỏi parabol nào là ảnh của (P) qua phép đối xứng trục Ox ?

A. \({x^2} = 12y\)                 

B. \({x^2} =  - 12y\)           

C. \({y^2} = 12x\)      

D. \({y^2} =  - 12x\)

Câu 7: Trong mặt phẳng với hệ trục tọa độ Oxy, cho phép đối xứng trục Oy, với \(M (x;y)\). Gọi \(M'\) là ảnh của M qua phép đối xứng trục Oy. Khi đó tọa độ điểm \(M'\) là:

A. \(M'(x;y)\)                        

B. \(M'( - x;y)\)                  

C. \(M'( - x; - y)\)      

D. \(M'(x; - y)\)

Câu 8: Hình nào sau đây có tâm đối xứng:

A. Hình thang                        

B. Hình tròn                      

C. Parabol                  

D. Tam giác bất kỳ

Câu 9: Trong mặt phẳng tọa độ Oxy, cho phép đối xứng tâm I (1;2) biến điểm M ( x;y) thành \(M'(x';y')\). Khi đó:

A. \(\left\{ {\matrix{ {x' =  - x + 2}  \cr{y' =  - y - 2}  \cr } } \right.\)   

B. \(\left\{ {\matrix{{x' =  -+ 2}  \cr {y' =  - y + 4}  \cr } } \right.\)

C. \(\left\{ {\matrix{ {x' =  - x + 2}  \cr  {y' =  - y - 4}  \cr} } \right.\)     

D. \(\left\{ {\matrix{{x' = x + 2}  \cr{y' = y - 2}\cr } } \right.\)

Câu 10: Trong mặt phẳng Oxy. Phép đối xứng tâm I (1;1) biến đường thẳng \(d:x + y + 2 = 0\) thành đường thẳng nào sau đây:

A. \(d':x + y + 4 = 0\)            

B. \(d:x + y + 6 = 0\)        

C. \(d:x + y - 6 = 0\)      

D. \(d:x + y = 0\)

Câu 11: Phép quay \({Q_{(o;\varphi )}}\) biến điểm M thành \(M'\). Khi đó

A. \(\overrightarrow {OM}  = \overrightarrow {OM'} \)và \((OM,OM') = \varphi \)      

B. \(OM = OM'\) và \((OM,OM') = \varphi \)

C. \(\overrightarrow {OM}  = \overrightarrow {OM'} \)và \(\widehat {MO\hat M'} = \varphi \)          

D. \(OM = OM'\) và \(\widehat {MOM'} = \varphi \)

Câu 12: Khẳng định nào sau đây đúng về phép quay.

A. Phép biến  hình biến điểm O thành O và điểm M khác điểm O thành điểm \(M'\)sao cho \((OM,OM') = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \).

B. Nếu \({Q_{(O;{{90}^0})}}:M \mapsto M'(M \ne O)\)thì \(OM' \bot OM.\)

C. Phép quay không phải là một phép dời hình.

D. Nếu \({Q_{(O;{{90}^0})}}:M \mapsto M'(M \ne O)\) thì \(OM' > OM.\)

Câu 13: Trong mặt phẳng Oxy cho điểm A ( 3;0). Tìm tọa độ ảnh \(A'\) của điểm A qua phép quay \({Q_{(o; - {\pi  \over 2})}}\).

A. \(A'( - 3;0)\)                      

B. \(A'(3;0)\)                     

C. \(A'(0; - 3)\)              

D. \(A'( - 2\sqrt 3 ;2\sqrt 3 )\)

Câu 14: Xét các mệnh đề sau:

(I): Phép dời hình biến 3 điểm không thẳng hàng thành 3 điểm không thẳng hàng.

(II): Cho 2 điểm phân biệt A,B và \(f\) là phép dời hình sao cho \(f(A) = A,f(B) = B\). Khi đó , nếu M nằm trên đường thẳng AB thì \(f(M) = M\)

(III): Phép dời hình biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác bằng tam giác bằng nó, biến đường tròn thành đường tròn bằng nó, biến góc thành góc bằng nó.

Số mệnh đề đúng trong 3 mệnh đề trên là:

A.0                                        

B. 1                                   

C. 2                                

D. 3

Câu 15: Nếu phép vị tự tỉ số k biến hai điểm M,N lần lượt thành hai điểm \(M',N'\) thì:

A. \(\overrightarrow {M'N'}  = k\overrightarrow {MN} \)và \(M'N' =  - kMN\) 

B. \(\overrightarrow {M'N'}  = k\overrightarrow {MN} \)và \(M'N' = \left| k \right|MN\)

C. \(\overrightarrow {M'N'}  = \left| k \right|\overrightarrow {MN} \)và \(M'N' = kMN\)

D. \(\overrightarrow {M'N'} //\overrightarrow {MN} \)và \(M'N' = {1 \over 2}MN\)

Câu 16: Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(x + y - 2 = 0\). Phép vị tự tâm O tỉ số \(k =-2\) biến d thành đường thẳng nào trong các đường thẳng có phương trình sau ?

A. \(2x + 2y = 0 \)

B. \(2x+ 2y - 4 = 0\)

C. \(x + y + 4 = 0\)                   

D. \(x +y - 4 = 0\)

Câu 17: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình \({(x - 1)^2} + {(y - 1)^2} = 4\). Phép vị tự tâm O tỉ số k = 2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?

A. \({(x - 1)^2} + {(y - 1)^2} = 8\)               

B. \({(x - 2)^2} + {(y - 2)^2} = 8\)

C. \({(x - 2)^2} + {(y - 2)^2} = 16\)     

D. \({(x + 2)^2} + {(y + 2)^2} = 16\)

Câu 18: Mọi phép dời hình cũng là phép đồng dạng tỉ số

A. \(k = 1\)                                  

B. \(k = -1\)                           

D. \( k = 0 \)                       

D. \(k = 3\)

Câu 19: Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường tròn (C) tâm \(I ( 3;2)\), bán kính R = 2. Gọi \((C')\) ảnh của (C) qua phép đồng dạng tỉ số k = 3. Khi đó trong các mệnh đề sau, mệnh đề nào sai ?

A. \((C')\) có phương trình \({(x - 3)^2} + {(y - 2)^2} = 36\)

B. \((C')\) có phương trình \({x^2} + {y^2} - 2y - 35 = 0\)

C. \((C')\) có phương trình \({x^2} + {y^2} + 2x - 36 = 0\)

D. \((C')\) có bán kính bằng 6.

Câu 20: Cho tam giác \(ABC\) đều với trọng tâm \(G\). Phép quay tâm \(G\) với góc nào dưới đây biến tam giác \(ABC\) thành chính nó?

A. \({30^0}\)                          

B. \({45^0}\)                           

C. \({60^0}\)                           

D. \({120^0}\)

Lời giải chi tiết

1B	2C	3B	4C	5D
6D	7B	8B	9B	10C
11B	12B	13C	14D	15B
16C	17C	18A	19C	20D

Câu 1:

Chỉ có duy nhất phép tịnh tiến theo vectơ \(\vec 0\) biến một đường tròn cho trước thành chính nó.

Chọn B.

Câu 2:

Gọi \(A'\left( {x';y'} \right)\)

Vì \({T_{\vec v}}\left( A \right) = A'\) nên \(\left\{ {\begin{array}{*{20}{c}}{x' = x + a}\\{y' = y + b}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x' = 1 - 3 =  - 2}\\{y' = 3 + 2 = 5}\end{array}} \right. \Rightarrow A'\left( { - 2;5} \right)\)

Chọn C.

Câu 3:

Lấy \(M\left( {x;y} \right) \in d\) tùy ý, ta có \(x - 1 = 0\,\,\,(1)\)

Gọi \(M'\left( {x';y'} \right) = {T_{\vec v}}(M) \Rightarrow M' \in d'\)

Vì \({T_{\vec v}}(M) = M'\) nên \(\left\{ {\begin{array}{*{20}{c}}{x' = x + 1}\\{y' = y + 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = x' - 1}\\{y = y' - 1}\end{array}} \right.\)

Thay vào (1) ta được \(x' - 1 - 1 = 0 \Leftrightarrow x' - 2 = 0\)

Mà \(M' \in d'\)

Vậy phương trình đường thẳng \(d'\)  là \(x - 2 = 0\)

Chọn B.

Câu 4:

\(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 16\).

Gọi \(\left( {C'} \right) = {T_{\vec v}}(C)\)

Lấy \(M\left( {x;y} \right) \in \left( C \right)\) tùy ý, ta có \(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 16\,\,\,\left( * \right)\)

Gọi \(M'\left( {x';y'} \right) = {T_{\vec v}}(M) \Rightarrow M' \in \left( {C'} \right)\)

Vì \({T_{\vec v}}(M) = M'\) nên \(\left\{ {\begin{array}{*{20}{c}}{x' = x + 1}\\{y' = y + 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = x' - 1}\\{y = y' - 3}\end{array}} \right.\)

Thay vào (*) ta được: \({\left( {x' - 3} \right)^2} + {\left( {y' - 4} \right)^2} = 16\)

Mà \(M' \in \left( {C'} \right)\)

Vậy phương trình đường tròn \(\left( {C'} \right)\)  là \({\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 16\)

Chọn C.

Câu 5:

Tam giác đều ABC có 3 trục đối xứng đó là ba đường trung trực của 3 cạnh.

Chọn D.

Câu 6:

Gọi \(\left( {P'} \right) = \)Đ_Ox (P).

Lấy \(M\left( {x;y} \right) \in \left( P \right)\) tùy ý, ta có \({y^2} =  - 12x\,\,\,(*)\)

Gọi \(M'\left( {x';y'} \right) = \)Đ_Ox(M) \( \Rightarrow M' \in \left( {P'} \right)\)

Vì Đ_Ox(M) = \(M'\) nên \(\left\{ {\begin{array}{*{20}{c}}{x' = x}\\{y' =  - y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = x'}\\{y =  - y'}\end{array}} \right.\)

Thay vào (*) ta được \({\left( { - y'} \right)^2} =  - 12x' \Leftrightarrow {y'^2} =  - 12x'\)

Mà \(M' \in \left( {P'} \right)\)

Vậy phương trình parabol \(\left( {P'} \right)\)  là : \({y^2} =  - 12x\)

Chọn D.

Câu 7:

Vì Đ_Oy(M) = \(M'\) nên \(\left\{ {\begin{array}{*{20}{c}}{{x_{M'}} =  - x}\\{{y_{M'}} = y}\end{array}} \right. \Rightarrow M'\left( { - x;y} \right)\)

Chọn B.

Câu 8:

Hình tròn có tâm đối xứng chính là tâm của hình tròn đó.

Chọn B.

Câu 9:

Vì Đ_I (M) = \(M'\) nên \(\left\{ {\begin{array}{*{20}{c}}{x' = 2.1 - x = 2 - x}\\{y' = 2.2 - y = 4 - y}\end{array}} \right.\)

Chọn B.

Câu 10:

Gọi \(d' = \)Đ­_I (d)

Lấy \(M\left( {x;y} \right) \in d\) tùy ý , ta có : \(x + y + 2 = 0\) (*)

Gọi \(M'\left( {x';y'} \right) = \)Đ_I(M) \( \Rightarrow M' \in d'\)

Vì Đ_I(M) = \(M'\) nên \(\left\{ {\begin{array}{*{20}{c}}{x' = 2 - x}\\{y' = 2 - y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 2 - x'}\\{y = 2 - y'}\end{array}} \right.\)

Thay vào (*) ta được : \(2 - x' + 2 - y' + 2 = 0 \Leftrightarrow x' + y' - 6 = 0\)

Mà \(M' \in d'\)

Vậy phương trình đường thẳng \(d'\)  là \(x + y - 6 = 0\)

Câu 11:

Vì \({Q_{\left( {O;\varphi } \right)}}\left( M \right) = M'\) nên \(\left\{ {\begin{array}{*{20}{c}}{OM = OM'}\\{\left( {OM,OM'} \right) = \varphi }\end{array}} \right.\)

Chọn B.

Câu 12:

Nếu \({Q_{\left( {O;{{90}^0}} \right)}}\left( M \right) = M'\,\,\left( {M \ne O} \right)\)  thì \(\left( {OM,OM'} \right) = {90^0}\) hay \(OM \bot OM'\)

Chọn B

Câu 13:

Gọi \(A'\left( {x';y'} \right)\)

Do \({Q_{\left( {O;\dfrac{{ - \pi }}{2}} \right)}}\left( A \right) = A'\)  nên \(\left\{ {\begin{array}{*{20}{c}}{x' = 0}\\{y' =  - 3}\end{array} \Rightarrow A'\left( {0; - 3} \right)} \right.\)

Chọn C.

Câu 14:

Cả 3 mệnh đề đều đúng

Chọn D.

Câu 15:

Theo tính chất của phép vị tự ta có: \(\overrightarrow {M'N'}  = k.\overrightarrow {MN} \) và \(M'N' = \left| k \right|MN\)

Chọn B.

Câu 16:

Gọi \(d' = {V_{\left( {O; - 2} \right)}}\,(d)\).

Lấy \(M\left( {x;y} \right) \in d\) tùy ý, ta có  \(x + y - 2 = 0\,\,\,\left( * \right)\)

Gọi \(M'\left( {x';y'} \right) = {V_{\left( {O; - 2} \right)}}\left( M \right) \Rightarrow M' \in d'\)

Vì \({V_{\left( {O; - 2} \right)}}\left( M \right) = M'\) nên \(\left\{ {\begin{array}{*{20}{c}}{x' =  - 2x}\\{y' =  - 2y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x =  - \dfrac{1}{2}x'}\\{y =  - \dfrac{1}{2}y'}\end{array}} \right.\)

Thay vào (*) ta được: \(\dfrac{{ - 1}}{2}x' + \dfrac{{ - 1}}{2}y' - 2 = 0 \Leftrightarrow x' + y' + 4 = 0\)

Mà \(M' \in d'\)

Vậy phương trình đường thẳng \(d'\)  là \(x + y + 4 = 0\)

Chọn C.

Câu 17:

Gọi \(\left( {C'} \right) = {V_{\left( {O;2} \right)}}\left( C \right)\).

Lấy \(M\left( {x;y} \right) \in (C)\) tùy ý , ta có \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4\,\,\,\left( * \right)\)

Gọi \(M'\left( {x';y'} \right) = {V_{\left( {O;2} \right)}}\left( M \right) \Rightarrow M' \in \left( {C'} \right)\)

Vì \({V_{\left( {O;2} \right)}}\left( M \right) = M'\) nên \(\left\{ {\begin{array}{*{20}{c}}{x' = 2x}\\{y' = 2y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \dfrac{{x'}}{2}}\\{y = \dfrac{{y'}}{2}}\end{array}} \right.\)

Thay vào (*) ta được:

 \(\begin{array}{l}{\left( {\dfrac{{x'}}{2} - 1} \right)^2} + {\left( {\dfrac{{y'}}{2} - 1} \right)^2} = 4 \Leftrightarrow \dfrac{{{{\left( {x' - 2} \right)}^2}}}{4} + \dfrac{{{{\left( {y' - 2} \right)}^2}}}{4} = 4\\ \Leftrightarrow {\left( {x' - 2} \right)^2} + {\left( {y' - 2} \right)^2} = 16\end{array}\)

Mà \(M' \in \left( {C'} \right)\)

Vậy phương trình đường tròn \(\left( {C'} \right)\)  là: \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 16\)

Chọn C.

Câu 18:

Mọi phép dời hình là phép đồng dạng  tỉ số k =1

Chọn A.

Câu 19:

\(\left( {C'} \right)\) là ảnh của \(\left( C \right)\) qua phép đồng dạng tỉ số k = 3 thì \(\left( {C'} \right)\) có bán kính \(R' = 3R = 6\)

Mà phương trình \(\left( {C'} \right):{x^2} + {y^2} + 2x - 36 = 0\) có bán kính \(R = \sqrt {37} \) nên đáp án C sai.

Chọn C.

Câu 20:

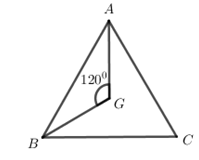
Ta thấy phép quay tâm \(G\) góc \({120^0}\) biến điểm \(A\) thành \(B\) , biến điểm \(B\) thành \(C\) và biến điểm \(C\) thành \(A\), do đó phép quay tâm \(G\) góc \({120^0}\) biến tam giác \(ABC\) thành chính nó.

Chọn D.