Câu hỏi 3 trang 48 SGK Hình học 12

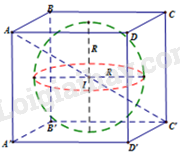
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy xác định tâm và bán kính mặt cầu:

LG a

a) Đi qua \(8\) đỉnh của hình lập phương.

Lời giải chi tiết:

Tâm mặt cầu là giao điểm các đường chéo.

Bán kính mặt cầu là \(OA = \displaystyle{1 \over 2}AC’\)

Đường chéo hình vuông cạnh \(a\) là \(AC = a\sqrt 2\)

Xét tam giác vuông \(ACC’\) tại \(C\):

Ta có: \(AC' = \sqrt {A{C^2} + C'{C^2}} \) \( = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {a^2}}  = a\sqrt 3 \)

Do đó \(AO = \dfrac{1}{2}AC' = \dfrac{{a\sqrt 3 }}{2}\).

Vậy bán kính mặt cầu đi qua \(8\) đỉnh hình lập phương cạnh \(a\) là \(R = \dfrac{{a\sqrt 3 }}{2}\).

LG b

b) Tiếp xúc với \(12\) cạnh của hình lập phương.

Lời giải chi tiết:

Không có mặt cầu tiếp xúc với \(12\) cạnh của hình lập phương.

LG c

c) Tiếp xúc với \(6\) mặt của hình lập phương.

Lời giải chi tiết:

Tâm mặt cầu tiếp xúc \(6\) mặt của hình lập phương là trung điểm \(I\) của đường nối hai tâm đáy.

Bán kính mặt cầu là \(r= \displaystyle{1 \over 2} AA’ \) \(=\displaystyle{a \over 2}\)