Câu 2 trang 211 SGK Giải tích 12 Nâng cao

LG a

Khảo sát sự biến thiên và vẽ đồ thị của hàm số f(x) = 2x³ – 3x² – 12x – 10

Giải chi tiết:

TXD: \(D =\mathbb R\)

f ’(x) = 6(x² – x – 2)

\(f'(x) = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr 
x = 2 \hfill \cr} \right.\)

Hàm số đạt cực đại tại \(x=1;\;y_{CĐ}=-3\)

Hàm số đạt cực tiểu tại \(x=2;\;y_{CĐ}=-30\)

\(\mathop {\lim }\limits_{x \to  \pm \infty } f(x) =  \pm \infty \)

Ta có bảng biến thiên:

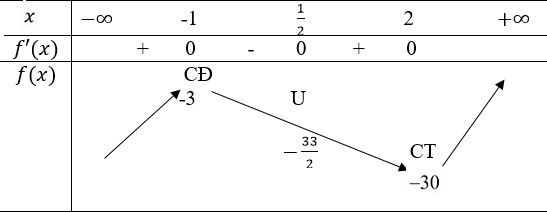
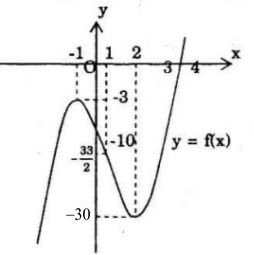
Đồ thị

LG b

Chứng minh rằng phương trình 2x³ – 3x² – 12x – 10 = 0 có nghiệm thực duy nhất.

Giải chi tiết:

Đồ thị hàm số y = 2x³ – 3x² – 12x – 10  cắt trục hoành tại một điểm duy nhất nên phương trình đã cho có nghiệm thực duy nhất.

LG c

Gọi nghiệm thực duy nhất của hàm số là \(α\).

Chứng ming rằnh \(3,5 < α < 3,6\).

Giải chi tiết:

Ta có: \(f(3, 5).f(3, 6) < 0\)

Vì vậy, phương trình có nghiệm \(α\)  duy nhất thỏa mãn điều kiện \(3,5 < α < 3,6\).