Câu 17 trang 213 SGK Giải tích 12 Nâng cao

Đề bài

Cho các số phức z₁ = 1 + i; z₂ = 1 – 2i

Hãy tính và biểu diễn hình học các số phức:

\(z_1^2;\,\,\,{z_1}{z_2};\,\,\,2{z_1} - {z_2}:\,\,{z_1}\overline {z_2};\,\,\,{{{z_2}} \over {\overline {z_1}}}\)

Lời giải chi tiết

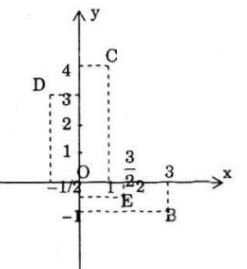
z₁² = (1 + i)² = 2i

z₁z₂ = (1 + i)(1 – 2i) = 3 – i

2z₁ – z₂ = 2(1 + i) – (1 – 2i) = 1 + 4i

\({z_1}\overline {{z_2}}  = (1 + i)(1 + 2i) =  - 1 + 3i\) 

 \({{{z_2}} \over {\overline {z_1}}} = {{1 - 2i} \over {1 - i}} = {{(1 - 2i)(1 + i)} \over 2} = {3 \over 2} - {i \over 2}\)