Bài 77 trang 135 Sách bài tập Hình học lớp 12 Nâng cao

Viết phương trình đường vuông góc chung của các cặp đường thẳng sau :

LG a

\(\eqalign{  & \;\;d:{{x - 2} \over 2} = {{y - 3} \over 3} = {{z + 4} \over { - 5}},\cr&\;\;\;\;\;d':{{x + 1} \over 3} = {{y - 4} \over { - 2}} = {{z - 4} \over { - 1}}\cr} \)

Lời giải chi tiết:

Cách 1: Ta có \(\overrightarrow {{u_d}}  = \left( {2;3; - 5} \right),\overrightarrow {{u_{d'}}}  = \left( {3; - 2; - 1} \right).\)

Khi đó vì \(\left[ {\overrightarrow {{u_d}} ,\overrightarrow {{u_{d'}}} } \right] = \left( { - 13; - 13; - 13} \right)\) nên đường vuông góc chung \(\Delta \) có một vectơ chỉ phương là \(\overrightarrow u  = \left( {1;1;1} \right).\)

Gọi \(\left( \alpha  \right)\) là mặt phẳng chứa d và \(\Delta \) thì \(\left( \alpha  \right)\) đi qua \({M_o}(2;3; - 4)\) và có vectơ pháp tuyến \(\overrightarrow {{n_\alpha }}  = \left[ {\overrightarrow {{u_d}} ,\overrightarrow u } \right] = \left( {8, - 7, - 1} \right).\)

Có phương trình của mp\(\left( \alpha  \right)\) là: \(8\left( {x - 2} \right) - 7\left( {y - 3} \right) - 1\left( {z + 4} \right) = 0\)

\( \Leftrightarrow 8x - 7y - z + 1 = 0.\)

Gọi \(\left( \beta  \right)\) là mặt phẳng chứa \(d'\) và \(\Delta \) thì \(\left( \beta  \right)\)  đi qua điểm \(M_o'\left( { - 1;4;4} \right)\) và có vectơ pháp tuyến \(\overrightarrow {{n_\beta }}  = \left[ {\overrightarrow u ,\overrightarrow {{u_{d'}}} } \right] = \left( {1;4; - 5} \right).\)

Phương trình của mp\(\left( \beta  \right)\) là :\(1\left( {x + 1} \right) + 4\left( {y - 4} \right) - 5\left( {z - 4} \right) = 0\)

\( \Leftrightarrow x + 4y - 5z + 5 = 0.\)

Vậy đường vuông góc chung \(\Delta \) của \(d\) và \(d'\) là giao tuyến của hai mặt phẳng \(\left( \alpha  \right)\) và \(\left( \beta  \right)\) . Nó có phương trình tham số là:

                               \(\left\{ \matrix{  x = t \hfill \cr  y = t \hfill \cr  z = 1 + t. \hfill \cr}  \right.\)

Cách 2: Điểm \(M \in d\) có toa độ là \(M = \left( {2 + 2t;3 + 3t; - 4 - 5t} \right).\)

Điểm \(N \in d'\) có toa độ là \(N = \left( { - 1 + 3t';4 - 2t';4 - t'} \right)\)

\( \Rightarrow \overrightarrow {MN}  = \left( { - 3 + 3t' - 2t;1 - 2t' - 3t;8 - t' + 5t} \right).\)

MN là đường vuông góc chung của \(d\) và \(d'\) khi và chỉ khi

 \(\left\{ \matrix{  \overrightarrow {MN} .\overrightarrow {{u_d}}  = 0 \hfill \cr  \overrightarrow {MN} .\overrightarrow {{u_{d'}}}  = 0 \hfill \cr}  \right.\)

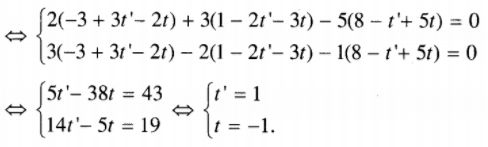
Suy ra \(M = \left( {0;0;1} \right),N = \left( {2;2;3} \right) \Rightarrow \overrightarrow {MN}  = \left( {2;2;2} \right).\)

Vậy phương trình chính tắc của đường vuông góc chung \(\Delta \) là

\({x \over 1} = {y \over 1} = {{z - 1} \over 1}.\)

LG b

\(\eqalign{  & \;\;d:\left\{ \matrix{  x = 2 + t \hfill \cr  y = 1 - t \hfill \cr  z = 2t \hfill \cr}  \right.,d':\left\{ \matrix{  x = 2 - 2t'. \hfill \cr  y = 3 \hfill \cr  z = t'. \hfill \cr}  \right. \cr} \)

Lời giải chi tiết:

\({{x - 2} \over 1} = {{y - 3} \over 5} = {z \over 2}.\)