Bài 5 trang 118 SGK Hình học 10 nâng cao

Đề bài

Một hình bình hành có hai cạnh nằm trên hai đường thẳng x + 3y - 6 = 0 và 2x - 5y - 1 = 0. Biết hình bình hành đó có tâm đối xứng là I(3, 5). Hãy viết phương trình hai cạnh còn lại của hình bình hành đó.

Lời giải chi tiết

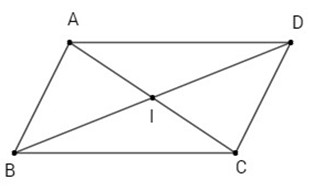
Giả sử hình bình hành ABCD có tâm I

\(\eqalign{
& AB:\,\,x + 3y - 6 = 0 \cr 
& AD:\,\,2x - 5y - 1 = 0 \cr} \) 

Tọa độ của A là nghiệm của hệ

\(\left\{ \matrix{
x + 3y - 6 = 0 \hfill \cr 
2x - 5y - 1 = 0 \hfill \cr} \right.\) \(\Leftrightarrow \,\,\,\left\{ \matrix{
x = 3\, \hfill \cr 
y = 1 \hfill \cr} \right.\)

Vậy \(A(3 ; 1)\).

I là trung điểm của AC nên

\(\left\{ \matrix{
{x_I} = {1 \over 2}({x_A} + {x_C}) \hfill \cr 
{y_I} = {1 \over 2}({y_A} + {y_C}) \hfill \cr} \right.\) \( \Leftrightarrow \,\,\left\{ \matrix{
{x_C} = 2{x_I} - {x_A} = 3 \hfill \cr 
{y_C} = 2{y_I} - {y_A} = 9 \hfill \cr} \right.\)

 Vậy \(C(3 ; 9)\).

BC là đường thẳng qua C(3;9) và song song với AD nên nhận (2;-5) làm VTPT

BC có phương trình:

\(2(x - 3) - 5(y - 9) = 0\) \(\Leftrightarrow 2x - 5y + 39 = 0\)

CD là đường thẳng qua C(3;9) và song song với AB nên nhận (1;3) làm VTPT

CD có phương trình:

\(1(x - 3) + 3(y - 9) = 0\) \( \Leftrightarrow x + 3y - 30 = 0\)

Vậy hai cạnh còn lại của hình bình hành là

\(2x - 5y + 39 = 0\) và \(x + 3y - 30 = 0\).

Cách khác:

Có thể viết pt BC và CD như sau:

*BC// AD nên BC có dạng: 2x – 5y + c = 0 (c ≠ -1).

Lại có C(3; 9) thuộc BC nên 2.3 – 5.9 + c = 0 ⇔ c = 39

Vậy BC: 2x – 5y + 39 = 0.

* Do CD// AB nên CD có dạng: x + 3y + d = 0 (d ≠ -6)

Do C(3; 9) thuộc CD nên : 3 + 3.9 + d= 0 ⇔ d = -30

Vậy CD: x + 3y - 30 = 0.