Bài 4.4 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức
Cho hình chóp tứ giác S.ABCD và M là một điểm thuộc cạnh SC (M khác S, C). Giả sử hai đường thẳng AB và CD cắt nhau tại N. Chứng minh rằng đường thẳng MN là giao tuyến của hai mặt phẳng (ABM) và (SCD).
Đề bài
Cho hình chóp tứ giác S.ABCD và M là một điểm thuộc cạnh SC (M khác S, C). Giả sử hai đường thẳng AB và CD cắt nhau tại N. Chứng minh rằng đường thẳng MN là giao tuyến của hai mặt phẳng (ABM) và (SCD).
Phương pháp giải - Xem chi tiết
Để chứng minh giao tuyến của hai mặt phẳng, ta tìm hai điểm cùng thuộc cả hai mặt phẳng đó.
Lời giải chi tiết
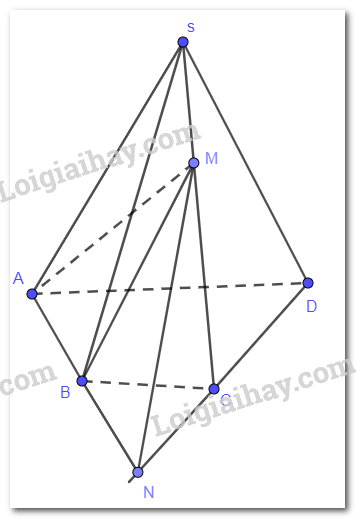
Ta có N thuộc đường thẳng AB , mà AB nằm trong mặt phẳng (ABM) nên N cũng nằm trong mp(ABM)
M và N đều nằm trong mặt phẳng (ABM) nên MN nằm trong mp(ABM) (1)
M thuộc SC suy ra M nằm trong mp(SCD), N thuộc đường thẳng CD nên N nằm trong mp(SCD)
Do đó, MN nằm trong mp(SCD) (2)
Từ (1) và (2) suy ra MN là giao tuyến của hai mp(ABM) và (SCD)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: " Bài 4.4 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: " Bài 4.4 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức timdapan.com"







