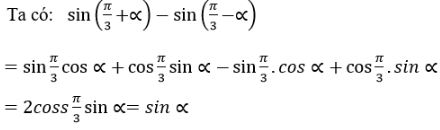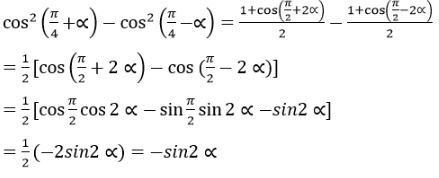Bài 44 trang 214 SGK Đại số 10 Nâng cao

Đơn giản các biểu thức sau:

LG a

\(\sin ({\pi  \over 3} + \alpha ) - \sin ({\pi  \over 3} - \alpha )\)

Phương pháp giải:

Sử dụng công thức \(\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\)

Lời giải chi tiết:

Ta có:

\(\sin ({\pi  \over 3} + \alpha ) - \sin ({\pi  \over 3} - \alpha ) \) \(= 2\cos \left( {\frac{{\frac{\pi }{3} + \alpha  + \frac{\pi }{3} - \alpha }}{2}} \right)\sin \left( {\frac{{\frac{\pi }{3} + \alpha  - \frac{\pi }{3} + \alpha }}{2}} \right)\) \(= 2\cos {\pi  \over 3}\sin \alpha  = \sin \alpha \)

Cách khác:

LG b

\({\cos ^2}({\pi  \over 4} + \alpha ) - {\cos ^2}({\pi  \over 4} - \alpha )\)

Phương pháp giải:

Sử dụng công thức hạ bậc \({\cos ^2}\alpha  = \frac{{1 + \cos 2\alpha }}{2}\)

Sử dụng công thức:

\(\begin{array}{l}
\cos \left( {\frac{\pi }{2} + \alpha } \right) = - \sin \alpha \\
\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha
\end{array}\)

Lời giải chi tiết:

Áp dụng: \({\cos ^2}a = {{1 + \cos 2a} \over 2}\) , ta có: 

\(\eqalign{
& {\cos ^2}({\pi \over 4} + \alpha ) - {\cos ^2}({\pi \over 4} - \alpha ) \cr&= {{1 + \cos ({\pi \over 2} + 2\alpha )} \over 2} - {{1 + \cos ({\pi \over 2} - 2\alpha )} \over 2} \cr} \)

\(\begin{array}{l}
= \frac{{1 - \sin 2\alpha }}{2} - \frac{{1 + \sin 2\alpha }}{2}\\
= \frac{1}{2} - \frac{{\sin 2\alpha }}{2} - \frac{1}{2} - \frac{{\sin 2\alpha }}{2}\\
= - \frac{{\sin 2\alpha }}{2} - \frac{{\sin 2\alpha }}{2}\\
= - \sin 2\alpha
\end{array}\)

Cách khác: