Bài 37 trang 123 SGK Toán 7 tập 1

Đề bài

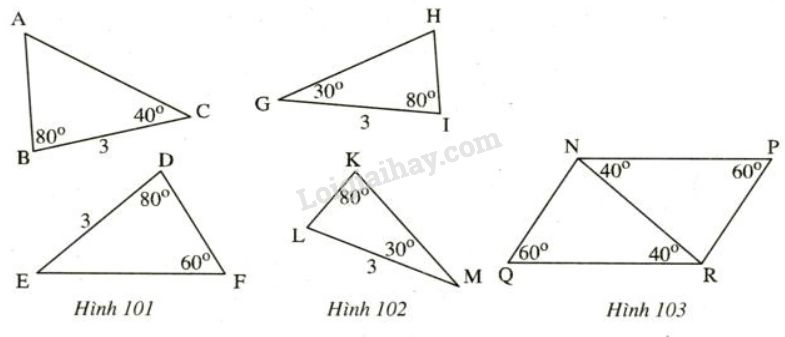
Trên mỗi hình 101, 102, 103 có tam giác nào bằng nhau? Vì sao?

Lời giải chi tiết

Tính các góc còn lại trên mỗi hình trên ta được:

Áp dụng định lí tổng ba góc của một tam giác ta có:

\(\eqalign{
& \widehat A = {180^0} - \widehat B - \widehat C\cr&\;\;\;\; = {180^0} - {80^0} - {40^0} = {60^0} \cr
& \widehat H = {180^0} - \widehat G - \widehat I \cr&\;\;\;\;\;= {180^0} - {30^0} - {80^0} = {70^0} \cr
& \widehat E = {180^0} - \widehat D - \widehat F \cr&\;\;\;\;= {180^0} - {80^0} - {60^0} = {40^0} \cr
& \widehat L = {180^0} - \widehat K - \widehat M \cr&\;\;\;\;= {180^0} - {80^0} - {30^0} = {70^0} \cr
& \widehat {QNR} = {180^0} - \widehat {NRQ} - \widehat {RQN} \cr&\;\;\;\;\;\;\;\;\;\;= {180^0} - {40^0} - {60^0} = {80^0} \cr
& \widehat {NRP} = {180^0} - \widehat {RPN} - \widehat {PNR}\cr&\;\;\;\;\;\;\;\;\;\; = {180^0} - {60^0} - {40^0} = {80^0} \cr} \)

- Xét \(∆ABC\) và \(∆FDE\) (Hình 101)

+) \(\widehat{B} = \widehat{D}=80^o\)

+) \(BC=DE=3\)

+) \(\widehat{C}=\widehat{E}=40^o\)

\( \Rightarrow ∆ABC=∆FDE\)  (g.c.g)

- Xét  \(∆NQR\) và \(∆RPN\) (Hình 103)

+) \(\widehat{QNR}=\widehat{NRP}=80^0\)

+) \(NR\) là cạnh chung.

+) \(\widehat{NRQ}=\widehat{RNP}=40^0\)

Suy ra \(∆NQR=∆RPN\)  (g.c.g)

- Xét \(\Delta HIG\) và \(\Delta LKM\) (Hình 102)

\(\eqalign{
& + )\,\,GI = ML \cr 
& + )\,\,\widehat G = \widehat M \cr 
& + )\,\,\widehat I = \widehat K \cr} \)

Ta có: \(\widehat G,\; \widehat I\) cùng kề với cạnh \(GI\), còn \(\widehat M \) kề với cạnh \(ML\) nhưng \( \widehat K\) không kề với cạnh \(ML\) nên \(\Delta HIG\) không bằng \(\Delta LKM\).