Bài 13 trang 46 SGK Đại số 10 nâng cao

Hàm số \(y = {1 \over x}\) có đồ thị như hình 2.10

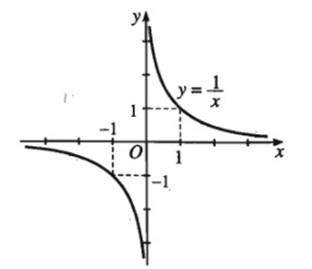
LG a

Dựa vào đồ thị, hãy lập bảng biến thiên của hàm số đó

Lời giải chi tiết:

Bảng biến thiên của hàm số

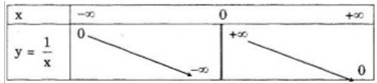
LG b

Bằng tính toán, hãy khảo sát sự biến thiên của hàm số trên khoảng  (-∞, 0) và (0, +∞) và kiểm tra lại kết quả so với bảng biến thiên đã lập.

Lời giải chi tiết:

Với x₁, x₂ ∈ \((-∞; 0)\) và x₁ ≠ x₂; ta có:

\(\begin{array}{l}
f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = \frac{1}{{{x_2}}} - \frac{1}{{{x_1}}} = \frac{{{x_1} - {x_2}}}{{{x_1}{x_2}}}\\
\Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \frac{{{x_1} - {x_2}}}{{{x_1}{x_2}}}:\frac{1}{{{x_2} - {x_1}}}\\
= - \frac{1}{{{x_1}{x_2}}} < 0
\end{array}\)

(vì x₁ < 0; x₂ < 0)

Vậy hàm số \(y = {1 \over x}\) nghịch biến trên \((-∞; 0)\)

Tương tự hàm số \(y = {1 \over x}\) cũng nghịch biến trên \((0; +∞)\)

Cách khác:

Với mọi x₁, x₂ ∈ (0; + ∞ ) ta có 0 < x₁ < x₂ => 1/x₁ > 1/x₂ 

Suy ra hàm số nghịch biến trên khoảng (0; + ∞ ).

Với mọi x₁, x₂ ∈ (- ∞; 0), ta có:

x₁ < x₂ < 0 => -x₁ > -x₂ > 0 => 1/(-x₁) < 1.(-x₂) => 1/x₁ > 1/x₂

Suy ra hàm số nghịch biến trên khoảng (- ∞; 0)