Bài 10 trang 191 SGK Đại số 10 Nâng cao
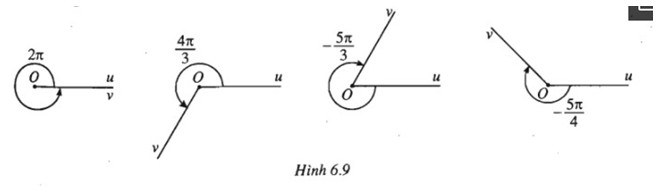
Tìm số đo radian α ,-π < α ≤π, của góc lượng giác có cùng tia đầu, tia cuối với góc trên mỗi hình sau.
Đề bài
Tìm số đo radian α ,-π < α ≤π, của góc lượng giác có cùng tia đầu, tia cuối với góc trên mỗi hình sau.
Lời giải chi tiết
a) Hình 1: Góc lượng giác có tia đầu Ou, tia cuối Ov có dạng: \(\alpha =2\pi +k2\pi\)
Ta có:
\(\begin{array}{l}
- \pi \le 2\pi + k2\pi \le \pi \\
\Leftrightarrow - 3\pi \le k2\pi \le - \pi \\
\Leftrightarrow - \frac{3}{2} \le k \le - \frac{1}{2}\\
\Rightarrow k = - 1\\
\Rightarrow \alpha = 2\pi - 2\pi = 0
\end{array}\)
b) Góc lượng giác có tia đầu Ou, tia cuối Ov có dạng: \(\alpha =\frac{{4\pi }}{3}+k2\pi\)
Ta có:
\(\begin{array}{l}
- \pi \le \frac{{4\pi }}{3} + k2\pi \le \pi \\
\Leftrightarrow - \frac{7}{3}\pi \le k2\pi \le - \frac{1}{3}\pi \\
\Leftrightarrow - \frac{7}{6} \le k \le - \frac{1}{6}\\
\Rightarrow k = - 1\\
\Rightarrow \alpha = \frac{{4\pi }}{3} - 2\pi = - \frac{{2\pi }}{3}
\end{array}\)
c) Góc lượng giác có tia đầu Ou, tia cuối Ov có dạng: \(\alpha =-\frac{{5\pi }}{3}+k2\pi\)
Ta có:
\(\begin{array}{l}
- \pi \le - \frac{{5\pi }}{3} + k2\pi \le \pi \\
\Leftrightarrow \frac{2}{3}\pi \le k2\pi \le \frac{8}{3}\pi \\
\Leftrightarrow \frac{1}{3} \le k \le \frac{4}{6}\\
\Rightarrow k = 1\\
\Rightarrow \alpha = - \frac{{5\pi }}{3} + 2\pi = \frac{\pi }{3}
\end{array}\)
d) Góc lượng giác có tia đầu Ou, tia cuối Ov có dạng: \(\alpha =-\frac{{5\pi }}{4}+k2\pi\)
Ta có:
\(\begin{array}{l}
- \pi \le - \frac{{5\pi }}{4} + k2\pi \le \pi \\
\Leftrightarrow \frac{1}{4}\pi \le k2\pi \le \frac{9}{4}\pi \\
\Leftrightarrow \frac{1}{8} \le k \le \frac{9}{8}\\
\Rightarrow k = 1\\
\Rightarrow \alpha = - \frac{{5\pi }}{4} + 2\pi = \frac{{3\pi }}{4}
\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 10 trang 191 SGK Đại số 10 Nâng cao timdapan.com"







