Bài 1 (4 điểm):

Giải hệ phương trình sau: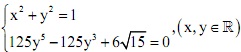

Bài 2 (4 điểm):

Cho dãy số (un) xác định bởi: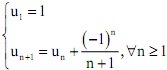

a. Chứng minh rằng:

b. Chứng minh rằng dãy số (u_n) có giới hạn hữu hạn, tìm giới hạn đó.

Bài 3 (3 điểm):

Hai đường tròn (O₁, R₁ ) và (O₂, R₂) (R₁ > R₂) cắt nhau tại hai điểm M và M’. Một tiếp tuyến chung T₁T₂ của hai đường tròn cắt đường thẳng O₁O₂ tại P (T₁ thuộc (O₁), T₂ thuộc (O₂)). Đường thẳng PM cắt (O₁) và (O₂) lần lượt tại M₁ và M₂ khác M. Đường thẳng PM’ cắt (O₁) và (O₂) lần lượt tại M₁’ và M₂’ khác M’. Gọi A, B, C, D lần lượt là trung điểm của MM₁, MM₂, M’M₁’, M’M₂’. Chứng minh rằng A, B, C, D nằm trên một đường tròn và đường tròn này tiếp xúc với T₁T₂.

Bài 4 (3 điểm):

Xác định các đa thức P(x) hệ số thực thỏa mãn P(x).P(x²) = P(x³+ 3x), ∀x thuộc R.

Bài 5 (3 điểm):

Cho hai số tự nhiên m và n sao cho m > n ≥ 1. Biết rằng hai chữ số tận cùng của 2014^m bằng với hai chữ số tận cùng của 2014ⁿ theo cùng thứ tự. Tìm các số m và n sao cho tổng m + n có giá trị nhỏ nhất.

Bài 6 (3 điểm)

Cho đa giác đều 9 đỉnh A₁A₂ ...A₉. Mỗi đỉnh của đa giác hoặc có màu đỏ hoặc có màu xanh. Chứng minh rằng tồn tại hai tam giác phân biệt bằng nhau có tất cả các đỉnh là các đỉnh của đa giác và cùng màu.